Nowe skanowanie 20080122081036 00000001E

4. Obwód elektryczny rozgałęziony prądu stałego Pytania

1. Uzasadnić możliwość zastąpienia rzeczywistego źródła napięcia równoważnym źródłem prądu.

2. Jaka jest moc wytwarzana wewnątrz źródła prądu I_ir zbocznikowanego rezystancją R_w: a) w stanie jałowym; b) w stanie zwarcia', c) przy obciążeniu rezystancją R?

3. Jakie warunki musi spełniać odbiornik rezystancyjny dopasowany do rzeczywistego źródła prądu

hr, R»?

4. Podać parametry rzeczywistego źródła napięcia równoważnego źródłu prądu l_ir zbocznikowanemu rezystancją R.

5. W których gałęziach i węzłach obwodu elektrycznego nie występują zmiany w wyniku jego przekształcenia drogą zamiany źródeł prądu na źródła napięcia i odwrotnie?

4.8. METODA OCZKOWA ROZWIĄZYWANIA OBWODÓW ELEKTRYCZNYCH

Liczba niezależnych równań Kirchhoffa, stanowiących podstawę analizy obwodu elektrycznego, jest równa liczbie gałęzi g w danym obwodzie. Składają się na nie równania prądowe w liczbie (w — 1) i równania napięciowe w liczbie n oznaczającej

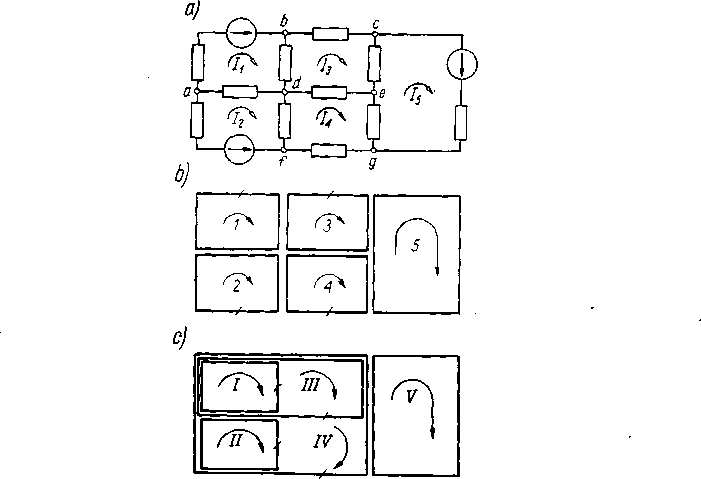
Rys, 4.18. Metoda prądów Oczkowych: a) schemat obwodu elektrycznego; b), c) przykłady doboru oczek niezależnych

liczbę niezależnych oczek. Do rozwiązania układu równań Kirchhoffa można zastosować dowolną ze znanych metod, np. metodę wyznaczników albo metodę kolejnego eliminowania równań. Ujmując eliminowanie równań w pewne systema-

4.S. Metóm ocznmoa

tyczne formy dochodzi się do nowych układów równań o mniejszej liczbie niewiadomych. Jedną z takich metod, polegającą na wyeliminowaniu równań prądowych i ograniczeniu się do równań napięciowych podał Maxwell. Jest ona znana pod nazwą metody prądów Oczkowych, prądów cyklicznych, lub krótko; metody oczkowej.

W celu objaśnienia stosowania metody oczkowej przyjęto konkretny obwód elektryczny, przedstawiony na rys. 4.18a, zawierający II gałęzi i 7 węzłów czyli g = 11; n = 7. Liczba niezależnych równań Oczkowych wynosi n = g — n +1 =5. Na rys. 4.18b podano najprostszy dobór oczek niezależnych biorąc po kolei oczka stykające się ze sobą. Skreślane po kolei gałęzie oznaczono kreskami poprzecznymi. Dla wszystkich oczek przyjęto obieg zegarowy.

Prądy w gałęziach a—b, b-c, c—g, g—fi f—a są równe prądom oczkowym ze znakiem ( + ) lub (—) zależnie od tego, czy mają zwroty zgodne ze zwrotami prądów Oczkowych, czy przeciwne. Prądy w pozostałych gałęziach są sumą lub różnicą prądów w oczkach, w skład których dana gałąź wchodzi, np. I_M = /_L — /₃,

Tfd — i Ą lo Itd.

Metoda oczkowa może być stosowana do rozwiązywania obwodów spełniających zasadę superpozycji, a więc obwodów liniowych.

Na rys. 4-18c przedstawiono inny podział obwodu na oczka tak pomyślany, aby dwie dowolnie dobrane gałęzie np. b — d i d—f wchodziły, każda w skład tylko jednego oczka. Oczka oznaczono dla odmiany cyframi rzymskimi I-yV w celu podkreślenia że prądy w nich są inne niż w oczkach na rys. 4-18b. Prąd w gałęzi a — b jest sumą aż 3 prądów Oczkowych: I_ah = U+Im + liy

Prądy w gałęziach c — e, b — d i f—d wynoszą: l_ce = l\n + hv — I\\ ha — h', Jfd = —h\-

Równania oczkowe można zapisać w bardzo przejrzystej i usystematyzowanej postaci ogólnej:

^11^1+^12^2 + ^13^3 + +^ln^ii ⁼ (?£)i

&21 11+R2212+&2S 11+ ... + R2nln — . 14TSS

R„lJj +R„2^2 + -Rn3^3+ ••• ^JrRnnh — (££)„

W równaniach (4.30): (2£)j = £} — suma napięć źródłowych w oczku j (./= 1,2Rjj — rezystancja własna oczka j, równa sumie rezystancji wszystkich gałęzi wchodzących w skład oczka j; R_kl = R_lk — rezystancja wzajemna oczka k i oczka i, tj. rezystancja gałęzi wspólnej dla oczek kil(k = 1, 2, ..., n; i = 1, 2, ..., n‘, k # /).

Rezystancje własne oczek podstawia się zawsze ze znakiem (+). Przy rezystancji wzajemnej R_kt = R,_k należy postawić znak ( + ), gdy zwroty prądów Oczkowych I_k, /, są w gałęzi wspólnej zgodne, zaś znak (—), gdy ich zwroty są przeciwne. W przypadku, gdy oczka k i / nie mają wspólnej gałęzi, należy podstawić R_kl = 0.