Nowe skanowanie 20080122070032 000000013 tif

4. Obwód elektryczny rozgałęziony prądu stałego

Konduktancja wewnętrzna G„ ■=■ }- = J _ = 0,4 S

J\ ^    J

Prąd w odbiorniku

l = C y ₌    50 G ₌    125    125

G+G_w *'    G+0,4    i 2,5+ R

2,5+    -

G

Wynik jest zgodny z wynikiem podanym w przykładzie 4.8.

Pytania

1.    Co to jest dwójnik? Podać przykłady dwójników.

2.    Kiedy dwójnik jest: a) pasywny; b) aktywny?

3.    Wykazać, że dowolny dwójnik aktywny liniowy można zastąpić rzeczywistym źródłem napięcia.

4.    Podać sformułowanie twierdzenia Thevenina.

5.    Jakie parametry charakteryzują dwójnik aktywny i jak można je wyznaczyć pomiarowo ?

6.    Czy pomiar dwóch stanów obciążenia: U, przy obciążeniu prądem h oraz U₂ przy prądzie Iz wystarcza do wyznaczenia parametrów dwójnika aktywnego ?

7.    Wyrazić słownie twierdzenie Nortona i wykazać jego słuszność.

8.    Kiedy korzysta się z twierdzenia Thevenina w rozwiązywaniu obwodów elektrycznych?

4.16. UKŁAD MOSTKOWY

W miernictwie elektrycznym jest bardzo rozpowszechniony układ mostkowy. Na rys. 4.35a pokazano schemat mostka Wheatstone’a.

Graf mostka przedstawia czworobok zupełny (rys. 4.Ib, c). Do zacisków a — b mostka przyłączone jest idealne źródło napięcia; w praktyce za źródło takie można

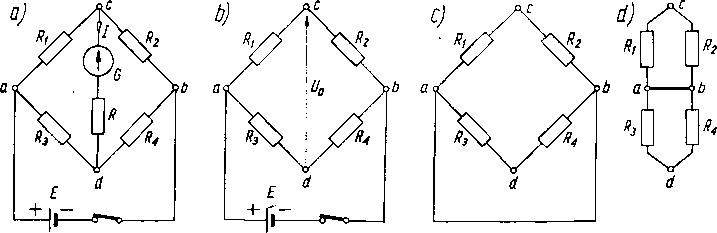
Rys. 4.35. Mostek Wheatstone’ą: a) układ mostka; b) mostek z wyłączoną gałęzią środkową; c), d) schematy do obliczania rezystancji wewnętrznej mostka mierzonej na zaciskach c—d

uważać akumulator, którego rezystancja wewnętrzna bywa znikomo mała w po; równaniu z innymi rezystancjami mostka. Między zaciski c — d włączony jest galwa-nometr (przyrząd reagujący na prąd rzędu 10^-9 do 10~⁷ A) oraz opornik chroniący galwanometr przed uszkodzeniem. Rezystancję gałęzi galwanometru oznaczono przez R, a rezystancje pozostałych gałęzi przez R_t, R₂, R₃, R*. Zadanie polega na wyznaczeniu prądu w gałęzi galwanometru.

Najwygodniej jest posłużyć się metodą Thevenina. W tym celu przedstawiono na rys. 4.35b układ do wyznaczenia napięcia U₀ między zaciskami c — d Uo = u_cd = V_c-V_d = (V_c-V_b)-(V_d-V_b) = U_cb-U_db

(4.55)

_ Rj__g_ R* p, _    R-2 R-3 R1R4 g

Ri+R₂ R₃ + Rą {R₁ + R₂){R₃ +^4)

Chcąc obliczyć rezystancję wewnętrzną układu, należy założyć, że E = 0. Wtedy zaciski a — b są połączone ze sobą bezrezystancyjnie (rys. 4.35c), ponieważ założono, że źródło napięcia jest idealne. Zaciski a — b można więc uważać jako zwarte ze-sobą, jak to pokazano na rys. 4.35d. Rezystancja tego układu, mierzona między zaciskami c — d

(4.56)

Ri R2__, R₃ R*

R₂~\~ R-2    źł₃+i?4

Prąd w gałęzi galwanometru wyraża się zależnością

j _    Uo ______R2 R3 ~ R1 Rą____g

R + R_w    R(R_t+R₂)(R3 +Rą) +R\ R₂(R₃ + Rą) + R₃ Rą(Ri+ R₂)

(4.57)

Mostek jest w równowadze, gdy przez galwanometr nie płynie prąd. Równowaga mostka zachodzi przy R₂ R₃ — Ri Rą = 0

tj-, gdy

(4.58)

R i_ _ R₃ r₂ r₄

Warunek równowagi mostka można wyznaczyć bezpośrednio, zakładając, że przez galwanometr nie płynie prąd, czyli, że potencjały punktów c i d są sobie równe (V_c = V_d). Ponieważ prąd 1=0, przez oporniki R_L i R₂ płynie ten sam prąd /,, a przez oporniki R₃ i R_A — prąd /₂. Z porównania napięć na opornikach wynika

R_lI_l=R₃I₂ R₂I i = Rą1₂

Dzieląc powyższe równania stronami przez siebie otrzymuje się podany wyżej wzór (4.58).

Łatwo sprawdzić, że równowaga mostka nie zostanie naruszona jeżeli źródło napięcia zostanie włączone między zaciski c — d, a galwanometr między zaciski a — b.

Mostek Wheatstone’a jest używany do pomiaru rezystancji. Jeżeli z czterech rezystancji w równaniu (4.58) trzy są znane, a mostek jest w równowadze, to czwartą rezystancję można obliczyć.

109