Nowe skanowanie 20080122070635 000000014 tif

16. Analiza obwodów prądu sinusoidalnego

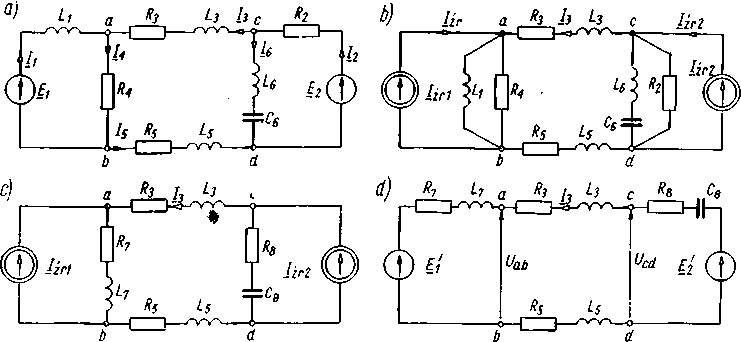
Rys. 16.9. Rysunek do przykładu 16.6: a) dany obwód; b, c, d) kolejne przekształcenie tego obwodu

ga-

Równoległe połączenia Rą, a>L_l oraz R₂, {^<»L₆--₀,c ) ^zast<iP^uj^emy pojedynczymi

łęziami (rys. 16.9c) o parametrach

R₇+jcoZ₇ = 1+j

1

coCs

= 2-j2

Zastępując źródło prądu równoważnymi źródłami napięcia o E[ = Itr i(R₂+}coL₇) = (24—j32) (1+j) = 56—j8

El

= (—9+jl2) (2 —j2) = 6+j42

oraz włączonymi w szereg impedancjami (R₇+jcoZ.₇)

i (Rs— j—* —) otrzymamy obwód nierozgałęziony (rys. 16.9d), w którym płynie prąd \ wt-ł /

h =

Ei-E;

(Rs + R₇ + R3 + R8)+j [ C0L5 + ojL₇-\- (0L3

_ 6+j42 — 56+j8 10+jl0

J5

cuC₈

Napięcia na zaciskach a, b i c, d w obwodzie (rys. 16.9d)

Uab — E[-\-{R-i ^Jr}(oL₁) [2 — 56— j8+j (1 +j) 5 = 51 —j3

Ua = El-^R_s -j —^-j/3 = 6+j42-j (2-j2) 5 = -4+J32

Prądy /₄, 7₆ obliczymy dzieląc napięcia U_ab i U_cd przez impedancje gałęzi 4 i 6 (rys. 16.9a) U =    = 25,5—j 1,5

-4+j32 j (6-10)

= -«-j

Prądy h, I₂ wyznaczymy z pierwszego prawa Kirchhoffa

U = U~h = 25,5 —j 1,5 —j 5 = 25,5—j6,5

/2 -    ły = —8—j+j5 = —8+j4

Wartości skuteczne prądów

Ii = 26,1 A; I₂ = 8,94 A; I₃ = 5 A;

U = 25,55 A; /_s = 5 A ;    /₆ = 8,06 A

Pytania

1.    Napisać wzory na przekształcenie trójkąta pasywnego impedancji na równoważną gwiazdę pasywną.

2.    Napisać wzory na przekształcenie gwiazdy pasywnej impedancji na trójkąt pasywny. Wykonać przekształcenie przyjmując:

a)    Zi = 30 Ci; Z₂ = j 30 Q; Z₃ = -j30 £1;

b)    Zi = Z₂ = Z₃ = (30+jI5) a

3.    Napisać wzory na przekształcenie trójkąta admitancji na gwiazdę admitancji i odwrotnie.

4.    Zamienić rzeczywiste źródło napięcia Ę o impedancji wewnętrznej Z„ — j A,„ na równoważne źródło prądu.

5.    Podać przykład przekształcania obwodu z zastosowaniem zamiany źródła napięcia na źródło prądu. Kiedy korzystne jest stosowanie takiej zamiany?

6.    Które prądy gałęziowe i potencjały węzłowe nie ulegają zmianie przy dokonywaniu przekształceń obwodu, jakkolwiek, ogólnie biorąc, prądy i potencjały zmieniają się?

16.6. TWIERDZENIE THEVENINA I NORTONA W ZASTOSOWANIU DO OBWODÓW PRĄDU SINUSOIDALNEGO

Znane z analizy sieci elektrycznych prądu stałego (rozdz. 4) twierdzenia Thevenina i Nortona są stosowane często także w analizie sieci zasilanych źródłami napięć i prądów sinusoidalnych pod warunkiem, że wszystkie elementy sieci są elementami liniowymi. W przypadku kilku źródeł zasilających daną sieć ich napięcia lub prądy źródłowe powinny odznaczać się jednakową częstotliwością, gdyż tylko wtedy prądy ustalone we wszystkich gałęziach sieci mają przebiegi sinusoidalne.

Rozważmy sieć elektryczną przedstawioną w układzie podanym na rys. 16.10n, w której za zaciski zasilające obraliśmy dwa dowolne zaciski a, b. Mamy za zadanie wyznaczyć zależność prądu / pobieranego przez odbiornik od jego impedancji Z. Obliczanie prądu / przy różnych wartościach Z przez rozwiązywanie równań Oczkowych lub węzłowych, gdy dane są parametry wszystkich elementów sieci, wymagałoby zbyt wielkiego nakładu pracy.

Zadanie można uprościć przez zastąpienie sieci zasilającej równoważnym idealnym źródłem napięcia i włączoną w szereg impedancją (twierdzenie Thevenina) lub źródłem prądu i włączoną równolegle impedancją (twierdzenie Nortona). W dal-

497

32 Podstawy elektrotechniki