Nowe skanowanie 20080122065025 00000000B tif

15. Analiza obwodów metodą liczb zespolonych

z którego otrzymujemy dwa równania 1

coC

coL ■

R

coL-

1

coC

= —R

Równania te mają dwa pierwiastki dodatnie

“■ = V Tc

R²

LC ⁺ 4L²

R

2L

R

2L

R² R    R

C ⁺ AL^{2 +}2L^X(°'⁺ 2L

(15.155)

(15.156)

(15.157)

(15.158)

ponieważ przy stosowanych możliwie małych rezystancjach w obwodach rezonanso wych

R² l    ,

, a więc w praktyce tylko nieznacznie wpływa na wartość pier-

4 L wiastka.

Szerokość pasma przepuszczania R

C0₂~C01 =

a ■ szerokość' względna-" ca, —co, R

(15.159)

(15.159a)

co_r co_rL

Im mniejsza jest rezystancja gałęzi R, L, C, tym węższe jest pasmo przepuszczania, a charakterystyka częstotliwościowa I = f(co) bardziej stroma, jak to pokazano na rys. 15.30, czyli selektywność obwodu jest większa.

W praktyce w gałęzi szeregowej R, L, C dostrajanej do rezonansu np. przez zmianę pojemności jedyną rezystancją jest zazwyczaj rezystancja cewki. Dlatego odwrotność prawej strony równania (15.159a) charakteryzującą daną cewkę nazwano dobrocią cewki, albo też dobrocią obwodu.

Dobroć cewki przy danej częstotliwości jest to stosunek jej reaktancji przy tej częstotliwości do jej rezystancji

coL _ 2nfL R~ R

Q =

(15.160)

Przykład 15.19. Dane są parametry układu szeregowego: R = 4 A; L = 200 p.H, C = 180 pF. Wyznaczyć częstotliwość rezonansową obwodu f_r, dobroć cewki Q oraz szerokość pasma przepuszczania.

Rozwiązanie. Częstotliwość rezonansowa 1 1

f' =-=

1tz\'lC 2tt)/200.10-M80-10-¹²

8,38 -10⁵ Hz.

f_r = 838 kHz

15.12. Rezonans napięć

I . fl fi

<»r    fr

Dobroć cewki

O    ₌ 27t-8,38-10⁵-200-\0 ⁶

^U R    R    4

Względna szerokość pasma przepuszczania

= --- = 0.0038 coL    263

skąd

/₂-/i = 0,0038-838 = 3,2 kHz

Gdyby rezystancja R = 40 ft, zamiast 4 O otrzymalibyśmy Q = 26,3 ; fi—fi = 32 kHz

15.12.4. DOPASOWANIE ODBIORNIKA DO ŹRÓDŁA O NAPIĘCIU SINUSOIDALNYM

Do źródła napięcia sinusoidalnego o napięciu źródłowym E i impedancji wewnętrznej Z,, = Rg+jA,, (wskaźnik g odpowiada nazwie łacińskiej źródła-generator) ma być przyłączony odbiornik o impedancji Z = R+']X (rys. I5.32a), dopasowanej ze względu na moc do danego źródła.

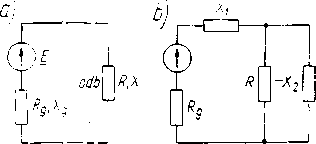
Rys. 15.32. Dopasowanie odbiornika do źródła napięcia sinusoidalnego: a) przy R = R_g; b) przy R = nR_g

Dopasowaniem odbiornika do źródła nazywamy taki dobór parametrów odbiornika, aby moc pobierana przez odbiornik z danego źródła była jak największa

P = RI^Z

XR+R_gr+(x+x_gr^E2

(15.161)

Chcąc wyznaczyć maksimum mocy w zależności od parametrów R, X należy zróżniczkować powyższe wyrażenie óraz względem X, drugi raz względem R i przyrównać obie pochodne do zera

c    R    —2R(X+X_g)

dx (R+R_gy+(x+x_g)²    [(R+R_gy+(x+x_g)²]²

Z przyrównania licznika do zera wynika warunek

Z=-A_g    '    (15.162)

identyczny, jak przy rezonansie napięć.

447