Nowe skanowanie 20080122064345 000000008 tif

ir. nnuivzu Uowuuuw

ważać praktycznie biorąc za źródło idealne, tj. takie, którego napięcie na za-skach nie zależy od prądu obciążenia. W rzeczywistych źródłach napięcia porni-ięcie impedancji wewnętrznej mogłoby spowodować duże błędy w obliczeniach rądów.

Napięcie U na zaciskach źródła rzeczywistego przy założeniu zgodnych zwrotów rzałek E, I (rys. 16.7a) wyraża się zależnością

U = E — Z_WI_    (16.17)

Źródła, w których napięcie E nie zależy od prądu obciążenia, a impedancja swnętrzna jest wielkością stałą, nazywamy, jak wiadomo, źródłami rzeczy-istymi liniowymi.

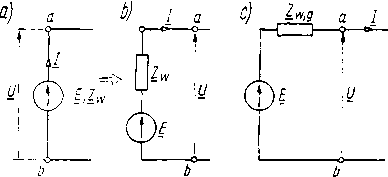
Rys. 16.7. Rzeczywiste źródło napięcia i równoważne źródło idealne z włączoną w szereg impedancją Z„ lub Z_wo

Ze wzoru (16.17) wynika, że każde rzeczywiste źródło napięcia można zastąpić :alnym źródłem napięcia z włączoną w szereg impedancją Z_w, równą impedancji wnętrznej źródła rzeczywistego (rys. 16.7b). Jeżeli gałąź, w której się znajduje idło rzeczywiste, zawiera jeszcze jakiś element impedancyjny Z_g, to możemy ją itąpić idealnym źródłem napięcia z włączoną w szereg impedancją Z_w + Z_g = Z_wg s. 16.7c).

Napięcie źródłowe E i impedancja wewnętrzna Z_w nie są częstokroć dane. teba je wyznaczyć na podstawie pomiarów. W przypadku źródła napięcia stałego jego scharakteryzowania wystarczą dwa pomiary: pomiar napięcia w stanie twym i pomiar prądu zwarcia lub rezystancji wewnętrznej. Do pomiaru napięcia rądu należy użyć przyrządów magnetoelektrycznych w celu wyznaczania zarówno rtości, jak i biegunowości.

Wyznaczenie napięcia zmiennego wymaga użycia oscylografu. Jeżeli wiemy, lany przebieg napięcia można z dostateczną dla celów praktycznych dokładnością rżać za sinusoidalny, ograniczamy się do pomiaru wartości skutecznej napięcia z pomiaru częstotliwości.

W przypadku kilku źródeł zasilających musimy znać kąty przesunięć fazowych dzy ich napięciami. Częstotliwość napięcia źródeł elektroenergetycznych mierzymy

itotliwościomierzem albo wyznaczamy ze wzoru / =    , jeżeli znana jest liczba

biegunów prądnicy oraz pomierzono prędkość obrotową.

Ib.b. Źródła napięcia i Jródla prądu

Drugim parametrem, który trzeba wyznaczyć jest impedancja wewnętrzna źródła Z,„. Z pomiarów napięcia stanu jałowego i prądu zwarcia można wyznaczyć jedynie moduł impedancji zespolonej Z_w = \Z_W\ = U₀/I_z. Jeżeli wiemy, że impedancja wewnętrzna źródła ma charakter rezystancyjno-indukcyjny, to zmierzywszy rezystancję R_w można wyznaczyć reaktancję wewnętrzną ze wzoru a>L_w =

Z równania (16.17) wynika, że przy obciążeniu źródła impedancją Z, napięcie na zaciskach źródła

u ^7 /;		(16.18)
Z+Zw
Po przekształceniu	równania (16.18) otrzymujemy
E U U	U
7 — ^ b y —	^+l i!W'	(16.19)

Pierwszy wyraz po prawej stronie równania (16.19) przedstawia prąd, który płynąłby przez impedancję Z_w włączoną na napięcie U, równolegle do Z; drugi wyraz jest prądem obciążenia / = U/Z-

Wyraz E/Z_w po lewej stronie równania przedstawia prąd, który musiałby dopływać do równolegle połączonych gałęzi o impedancjach Zw, Z ze źródła prądu.

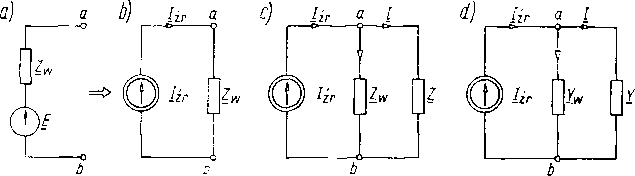
Rys. 16.8. Źródło napięcia i równoważne źródło prądu: a) źródło napięcia; b) źródło prądu nie obciążone; c, d) źródło obciążone impedancją Z lub admitancją Y

Rzeczywiste źródło napięcia E o impedancji wewnętrznej Z_w można zastąpić źródłem prądu I_ir = EJZw zbocznikowanym impedancją Z_w (rys. 16.8a, b).

Jeżeli źródło prądu obciążymy impedancją Z, to prąd obciążenia (rys. 16.8c, d):

(16.20)

/ = I,

7-_{w    =}    Y

Z+Z_w ^ir Y + Y_w

Przykład 16.6. Obliczyć prądy w układzie przedstawionym na rys. 16.9a zastępując źródła napięcia równoważnymi źródłami prądu.

Dane: wLt — 2 O; R₂ =- 4 O; R₃ = 3 O; wL₃ = 3 O; i?₄ = 2 Q; R₅ = 4 Q; (oL_s = = 8 0; o)L₆ = 6 O; l/OC₆) = 10 Q; E_l = 64-kj 48; E₂ = — 36+j 48

Danemu układowi odpowiada układ równoważny, przedstawiony na rys. 16.9b, w którym prądy źródłowe

Itr 1 = —= ^⁴⁺ji⁸ = 24—j32 jwLi    j2

L_r ,    '-²- : : ”³⁽' ^{i ,S} . = -9+jl2

R₂    4

495