Nowe skanowanie 20080122065606 00000000F tif
4. Obwód elektryczny rozgałęziony prądu stałego
napięcia E' i element rezystancyjny R, gdyż prąd 1 nie spowoduje na przewodzie zwierającym żadnego spadku napięcia. Ostatecznie pozostanie gałąź a — b zawierająca tylko źródło idealne o napięciu źródłowym E = RI (rys. 4.29c) zastępujące odbiornik R. Stąd wynika następujące twierdzenie o kompensacji.
Rozpływ prądów u- obwodzie elektrycznym nie ulegnie zmianie, jeżeli dowolny element rezystancyjny R tego obwodu zostanie zastąpiony źródłem idealnym o napięciu źródłowym E równym spadkowi napięcia RI na tym elemencie i o zwrocie przeciwnym niż zwrot prądu I.
Należy podkreślić, że danym napięciem źródłowym E można skompensować napięcie na elemencie rezystancyjnym R tylko przy jednej wartości prądu I. Ze zmianą prądu I musi się zmieniać wartość, a nawet i zwrot napięcia E, jeżeli wartość prądu I jest ujemna.
Napięcie źródłowe, którego wartość i zwrot zależą od prądu płynącego przez źródło nazywa się napięciem źródłowym sterowanym.
Napięcie źródłowe, którego wartość i zwrot nie zależą od prądu płynącego przez źródło, nazywa się napięciem źródłowym niesterowanym.
Element rezystancyjny R, przez który płynie prąd /, można zastąpić idealnym źródłem napięcia o napięciu źródłowym sterowanym: E = RI.
Twierdzenie o kompensacji bywa powszechnie stosowane w metodzie składowych symetrycznych (zob. rozdz. 20).
Pytania
1. Sformułować twierdzenie o kompensacji i udowodnić jego słuszność.
2. Dlaczego kompensujące źródło napięcia musi być źródłem idealnym ?
3. Podać określenia napięć źródłowych idealnych: a) sterowanego; b) niesterowanego.
4.13. ROZWIĄZYWANIE OBWODÓW ELEKTRYCZNYCH METODĄ SUPERPOZYCJI
Zgodnie z zasadą superpozycji prąd w dowolnej gałęzi bądź potencjał dowolnego węzła obwodu liniowego zasilanego przez dowolną liczbę idealnych źródeł napięcia i źródeł prądu jesft sumą prądów w tej gałęzi bądź potencjałów w tym węźle wywołanych przez każde z tych źródeł działające oddzielnie.
Jeżeli w obwodzie znajdują się rzeczywiste źródła napięcia, należy je zastąpić źródłami idealnymi, a ich rezystancje wewnętrzne dodać do rezystancji odpowiednich gałęzi obwodu. f
Metodę superpozycji można stosować do rozwiązywania obwodów elektrycznych. W tym celu oblicza się prądy w gałęziach lub potencjały węzłów, pochodzące od poszczególnych źródeł zakładając, że wszystkie inne źródła mają napięcia źródłowe ,
4.13. Rozwiązywanie metodą superpozycji
i prądy źródłowe równe zeru, ale ich rezystancje wewnętrzne i bocznikujące pozostają w obwodzie. Otrzymane wyniki dodaje się algebraicznie.
Przykład 4.7. Obliczyć prądy w obwodzie przedstawionym na rys. 4.30a stosując metodę superpozycji. Dane: £, = 54 V, Rwl = 1 £2, TC, = 5 £2, R2 = 18 0, R3 = 9 £2, = 6 A.
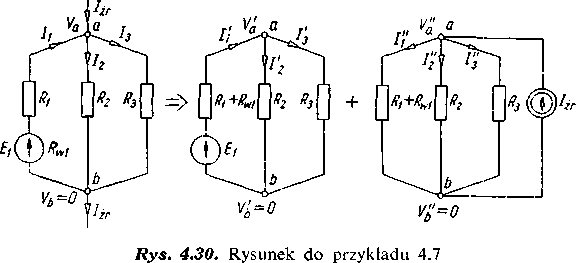
Rozwiązanie. Stan danego obwodu przedstawiono jako superpozycję dwóch stanów: a) przy zasilaniu źródłem napięcia Et, przy czym rezystancję wewnętrzną Rwi dodano do rezystancji gałęzi Ri; b) przy zasilaniu źródłem prądu włączonym między zaciski a — b.
W obu przypadkach korzystnie jest zastosować metodę węzłową, która przy założeniu Vb = O prowadzi do równania o jednej niewiadomej tj. potencjału w węźle a.
a)
1
Ri + R„i
= A54 6
I1 t 1 ; M Kj
\ 6 18 9/
V'a = 27 V
= hr
b) [-1---+ — - + --W
KRi + Rwi Rz RA
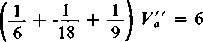
V'a' = 18 V
Potencjał węzła a jest sumą obu potencjałów
Pa= v'a + V'a
Va = 45 V
Poszczególne prądy:
/ 2
K Vb
Rz
45
18
= 2,5
A
h=JA=A^ = AI = 5 a R3 9
h = Iz + h-hr = 2,5 + 5-6 = 1,5 A
7* 99
Wyszukiwarka
Podobne podstrony:
Nowe skanowanie 20080122065857 000000011 tif 4. Obwód elektryczny rozgałęziony prądu stałego napięci
Nowe skanowanie 20080122065408 00000000D tif 4. Obwód elektryczny rozgałęziony prądu stałego Korzyst
Nowe skanowanie 20080122065508 00000000E tif 4. Obwód elektryczny rozgałęziony prądu stałego gałęzie
Nowe skanowanie 20080122065813 000000010 tif 4. Obwód elektryczny rozgałęziony prądu stałego Amperom
Nowe skanowanie 20080122065953 000000012 tif 4. Obwód elektryczny rozgałęziony prądu stałego wykonuj
Nowe skanowanie 20080122070032 000000013 tif 4. Obwód elektryczny rozgałęziony prądu stałego Kondukt
Nowe skanowanie 20080122063917 000000005 tif 3. Obwód elektryczny nierozgałęzionyPytania 1. &n
Nowe skanowanie 20080122064027 000000006 tif 3. Obwód elektryczny nierozgałęziony nicznej, energia c
Nowe skanowanie 20080122064141 000000007 tif 3. Obwód elektryczny nierozgałęziony Przykład 3.7. Obli
Nowe skanowanie 20080122064728 00000000A tif 3. Obwód elektryczny nierozgałęziony Pytania 1. &
Nowe skanowanie 20080122070635 000000014 tif 16. Analiza obwodów prądu sinusoidalnego Rys. 16.9. Rys
Nowe skanowanie 20080122070737 000000016 tif 16. Analiza obwodów prądu sinusoidalnego Prąd wyznaczon
Nowe skanowanie 20080122070806 000000017 tif 16. Analiza obwodów prądu sinusoidalnego soidalnym o st
więcej podobnych podstron