Nowe skanowanie 20080122070707 000000015 tif

szym ciągu będziemy się opierali na wzorach wyprowadzonych w rozdz. 4, posługując się w przypadku wymuszeń sinusoidalnych metodą liczb zespolonych.

Prąd płynący przez odbiornik o impedancji Z wyraża się zależnością

(16.21)

/ ₌ & ₌ _ JL_

Z+Z_w Z+Zw

stanowiącą analityczne ujęcie twierdzenia Thevenina, które można sformułować następująco:    ¹

Każdą sieć elektryczną liniową zawierającą wyłącznie źródła napięcia lub prądu sinusoidalnego o jednakowej częstotliwości, traktowaną jako źródło zasilające o dowolnie wybranych zaciskach a i b, można przy danej częstotliwości f zastąpić równoważnym idealnym źródłem napięcia Ez włączoną w szereg impedancją Z_w (^ry^s- 16.lOb).

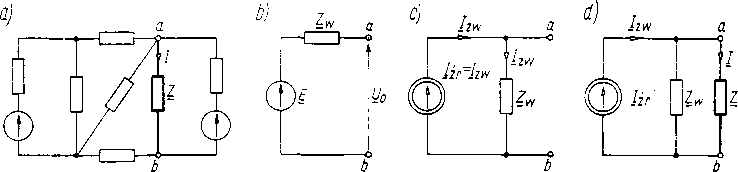
Rys. 16.10. Sieć elektryczna: a) obciążona na zaciskach a, b impedancją Z; b) równoważne źródło napięcia nie obciążone; c, d) równoważne źródło prądu nie obciążone oraz obciążone impedancją Z

Napięcie źródłowe E jest równe napięciu U₀ mierzonemu na zaciskach a, b w stanie jałowym, tj. przed włączeniem odbiornika Z. Impedancją Z,_v jest równa impedancji wewnętrznej sieci, mierzonej na zaciskach a, b przy założeniu, że wszystkie napięcia i prądy źródłowe sieci są równe zeru, ale że impedancje wewnętrzne źródeł napięcia, jak również impedancje bocznikujące źródła prądu pozostają w sieci bez zmiany.

Impedancję Z_w można obliczyć znając schemat sieci oraz impedancje poszczególnych elementów sieci. Jeżeli jest brak danych potrzebnych do obliczenia impedancji Z_w, można ją wyznaczyć laboratoryjnie. W tym celu należy wyłączyć z sieci wszystkie napięcia źródłowe, zastępując je ich impedancjami wewnętrznymi. Następnie do rozpatrywanych zacisków sieci a, b należy doprowadzić z zewnątrz napięcie sinusoidalne o częstotliwości tej samej jak częstotliwość, przy której ma odbywać się praca sieci i zmierzyć wartości skuteczne napięcia oraz prądu, a także moce czynną i bierną, pobierane przez sieć podczas pomiaru. Ze stosunku U/I wyznaczamy moduł impedancji Z_w = |ZJ, a ze stosunku Q/P wyznaczamy tg <p_w. Impedancją wewnętrzna zespolona Z_w = Z_w e^iiPw.

Gdy impedancją obciążenia Z -> 0, to prąd

llo

Zw

skąd

Z,

Uo

L

(16.22)

Prąd zwarcia jest prądem źródłowym przy zamianie danej sieci na równoważne źródło prądu (rys. 16.10c). Z równania (16.21) otrzymujemy zależność

Iż0_ Zw

ZI , u

+l=~-

+ /

(16.23)

w której U₀jZ_w = l_z przedstawia prąd źródłowy L_r dopływający do równolegle połączonych impedancji Z_w i Z (rys. 16.1 Od). Z równania (16.23) otrzymujemy łatwo zależność prądu obciążenia I od prądu źródłowego

l=hr

Z+Z»

= /.

z+z„

(16.24)

albo

y+y_k

(16.24a)

Wzory (16.23), (16.24) i (16.24a) są analitycznymi wyrażeniami twierdzenia Nortona dotyczącego sieci prądów sinusoidalnych.

Każdą sieć elektryczną liniową, zawierającą wyłącznie źródła napięcia lub prądu sinusoidalnego o jednakowej częstotliwości, traktowaną jako źródło zasilające o dowolnie wybranych dwóch zaciskach a, b, można przy danej częstotliwości f zastąpić źródłem prądu l_ir z włączoną równolegle impedancją Z_w.

Prąd źródłowy L_r jest równy prądowi zwarcia I. mierzonemu na zaciskach a, b Impedancją Z_w jest impedancją wewnętrzną sieci, mierzoną na zaciskach a, b przy usunięciu z sieci wszystkich źródeł napięcia i prądu, lecz przy pozostawieniu ich impedancji wewnętrznych (w przypadku źródeł napięcia) lub bocznikujących (w przypadku źródeł prądu).

Przykład 16.7 Do zacisków c, d sieci z przykładu 16.6 ma być włączony odbiornik o impedancji Z. Wyznaczyć zależność prądu I pobieranego przez odbiornik od jego impedancji Z

32*

Rozwiązanie I. Rozpatrywaną sieć sprowadzono w przykładzie 16.6 do obwodu nierozgałęzionego (rys. 16.9d), którego parametry po zastąpieniu połączonych szeregowo impedancji (7?, \ R_t ~-R₇)+}l(oL₁ + (oL₃ + (oL₁) jedną impedancją Z_g, są następujące (rys. 16.11 a): E\ 56 jS; = 6+j42; Z_g = 8+jl2 oraz Z₈ = 2—j2.

Rys. 16.11. Obwód omawiany w przykładzie 16.7: a) nie obciążony na zaciskach c, d; b) obciążony impedancją Z\ c) zwarty na zaciskach c, d

499