Nowe skanowanie 20080122081159 000000020

16. Analiza obwodów elektrycznych prądu sinusoidalnego

16.1. RÓWNANIA OGÓLNE OBWODÓW ELEKTRYCZNYCH PRĄDU SINUSOIDALNEGO

Do przeprowadzenia analizy obwodów elektrycznych złożonych czyli sieci elektrycznych nie wystarcza umiejętność obliczania obwodów zawierających wyłącznie połączone szeregowo albo równolegle elementy impedancyjne. Musimy korzystać z równań Kirchhoffa, stanowiących bazę wyjściową w rozwoju teorii obwodów elektrycznych.

Zajmiemy się wyłącznie obwodami liniowymi, w których wszystkie parametry obwodu R, L, C, jak również rezystancje i impedancje wewnętrzne źródeł napięcia, są wielkościami stałymi a przebiegi napięć zasilających są niezależne od prądu obciążenia. Zakładamy ponadto, że wszystkie parametry obwodu elektrycznego (sieci elektrycznej) są skupione. W tych warunkach można stosować zasadę superpozycji. Przy pominięciu ładunków początkowych na kondensatorach

£ i = 0

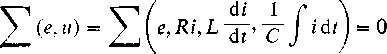
Jeżeli w rozpatrywanej sieci elektrycznej działa tylko jedno źródło o napięciu sinusoidalnym e = E,„ sin (oh+ yv), to prądy ustalone we wszystkich gałęziach tej sieci mają przebiegi sinusoidalne o tej samej pulsacji to.

Dowód, który pomijamy, wynika bezpośrednio z rozwiązania równań różnicz-kowo-całkowych Kirchhoffa za pomocą rachunku operatorowego. Prąd w dowolnej gałęzi otrzymuje się jako sumę dwóch prądów: jednego o przebiegu sinusoidalnym i pulsacji to, stanowiącego tzw. prąd ustalony i drugiego — zanikającego wykładniczo, praktycznie biorąc, w ciągu ułamków sekundy.

Gdy sieć jest zasilana przez kilka źródeł napięcia sinusoidalnego o jednakowej częstotliwości, to prąd ustalony w dowolnej gałęzi sieci, będący przy uwzględnieniu zasady superpozycji sumą wywołanych przez poszczególne źródła prądów składowych sinusoidalnych o tej samej częstotliwości, jest również sinusoidalny o tej

16.1. Równania ogólne

samej częstotliwości. Dzięki temu do analizy stanów ustalonych w sieciach elektrycznych zasilanych przez dowolną liczbę źródeł napięcia sinusoidalnego o jednakowej częstotliwości można stosować metodę liczb zespolonych, przy której stosowaniu:

a) operacjom różniczkowym i całkowym odpowiadają operacje algebraiczne mnożenia i dzielenia przez jco;

b) wszystkim operacjom algebraicznym na funkcjach zespolonych odpowiadają identyczne operacje na wartościach zespolonych.

W konsekwencji równaniom Kirchhoffa w postaci różniczkowo-całkowej odpowiadają przy stosowaniu rachunku liczb zespolonych, analogicznie do równań w sieciach prądu stałego, równania w postaci algebraicznej

17 = 0

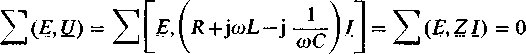
(16.1)

(16.2)

Chcąc np. wyznaczyć rozpływ prądów w sieci prądu sinusoidalnego musimy znać wszystkie napięcia źródłowe £ działające w danej sieci, tzn. znać zarówno ich wartości skuteczne, jak i fazy początkowe.

Gdy w danej sieci działa tylko jedno źródło napięcia, nie podaje się najczęściej fazy początkowej, ponieważ nie wpływa ona ani na wartości skuteczne prądów, ani na kąty przesunięć fazowych między poszczególnymi prądami lub między prądami a napięciem zasilającym. Wówczas, przystępując do wyznaczenia rozpływu prądów, obiera się dowolnie fazę początkową napięcia, np. y>_e = 0, co odpowiada położeniu wektora £ w osi rzeczywistej (£ = £), lub y>_e = 90°, odpowiadające położeniu wektora £ w osi urojonej (£ = j£). Wektor £ stanowi tzw. wektor podstawowy, którego położenie powinno być ustalone przed przystąpieniem do rozwiązywania zadania.

W przypadku kilku źródeł napięcia działających w danej sieci rozpływ prądów zależy nie tylko od wartości skutecznych napięć źródłowych, ale także od kątów przesunięć fazowych między tymi napięciami. Wobec tego znajomość faz początkowych jest niezbędna do rozwiązania zadania. Jeżeli dane są tylko przesunięcia fazowe między poszczególnymi napięciami, należy fazę początkową jednego z napięć obrać dowolnie, a fazy pozostałych napięć źródłowych ustalić na podstawie danych przesunięć fazowych.

Przykład 16.1. W sieci są trzy źródła napięcia o wartościach skutecznych: E₁ = 450 V; E₂ -= 400 V; E₃ — 500 V, przy czym wiadomo, że napięcie e₂ jest przesunięte w przód o 30', a napięcie e₃ — wstecz o 60° względem napięcia e_s.

Podać wartości zespolone napięć E_u E₂ i E₃, które trzeba podstawić w równaniach Kirchhoffa dla danej sieci.

Rozwiązanie. Przyjmijmy £i za wektor podstawowy w osi urojonej

= j450

■■ Ei e

31* 483