022 #

Redukcja układu sił do wektora głównego i momentu głównego.

K>x e> -5 [Vmni(0( «• ci tura gtomłcęo R t punktu A lio dowolnego punktu O

6.1. Warunki równowagi dowolnego płaskiego układu sił

Ahj¹ dcuelny płmki układ sil znajdował się iv równowadze zarówno wektor główny R. jak i moment główny M muszą być równe zeru. /Mcm składowe wektora R oraz suma momentów względem dowolnego punktu muszą byt równe zeru. Warunki równowagi w przypadku płaskiego układu sił sprów-ndząfij się du spełnienia układu równań.

=°    Ś^/»=°    Ż"--°    «*U

Powyższe równania nazywamy równaniami równowagi dla płaskiego d6-wołnego układu sil. Równania te służą do obliczania reakcji w punktach podparcia konstrukcji < belki. płyty). Aby obliczyć reakcje na podporach, uwalniamy konstrukcję od więzów, wprowadzając wektory sił odpowiadające sposobowi podparcia oraz piszemy równania równowagi. Jeżeli po rozwiązaniu układu równań okaże się. żjc utrzymaliśmy ujeiiuic wartości sil lub momentów, to znaczy, /c ztwuy ul tcógi w rzeczy wistości są skierowane w przeciwną stronę.

7. 'Farcie i prawa tarcia

Podstawy loorclyc/nc dotyczące zagadnień uucia przedstawione poniżej dotyczą izw. l.mjfl statycznego, przy założeniu bardzo małych prędkości przesuwających się ciał Zagadnienia dotyczące tarcia kinetycznego wymagają oddzielnego omówienia j wykraczają poza program niniejszego skryptu.

Prawa tarcia

I Wartość riły tarcia nic zalety od wielkości stykających się powierzchni, ale od kh rodzaju (rodzaj powierzchni, stan chrnpowaiości iip.)

2. Wartość siły tarcia T zalety od nacisku normalnego i zawiera sic w granicach

(7.1)

0<;7W_to =\l-S

3. Zw rot siły tarcia jest przeciwny do zamierzonego kierunku cuchu

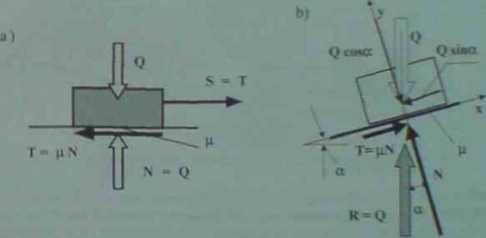
Rys 7 I. Slh tarcia, at tu pbsrers .-nie. h| na ro»m jwdiyig

W przypadku ciała, którego wymiary są pomijalmc maić. tak żc można je sprowadzić do punktu materialnego irys. 7.1> mI> działające na cjąfo nwina w przybliżeniu potraktować jako układ sil zbieżnych. Równania równowagi, na podstawie których oblicza się współczynnik tarcia fi dla ciała umieszczonego na równi nachylonej pod kątem u mąją postać

I «l

* Q-sln a = p • 1? \cwtt    skąd

23