18 (84)
Fit/Y,'^' f



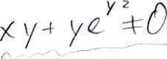
V Ti x/4 T /

Traktując lewą stronę równości jako funkcję jednej zmiennej x i stosując twierdzenie o różniczkowaniu takiej funkcji otrzymamy:

dx dx dy ax hy(x,yj
dF dx + dF
Różniczkując powyższą równość stronami po zmiennej x, otrzymamy wzór na drugą pochodną funkcji uwikłanej jednej zmiennej:
\ y W" /CM3
Wykorzystując wzór na pierwszą pochodną funkcji uwikłanej oraz twierdzenie Fermata (warunek konieczny istnienia ekstremum) możemy podać warunki, na podstawie których możemy wyznaczyć punkty stacjonarne:

18 MAT2 Mechatronika Jan Nawrocki
Wyszukiwarka
Podobne podstrony:
84 II. Funkcje jednej zmiennej Nie należy przy tym sądzić, że zachodzi istotna różnica pomiędzy funk
PB072359 53 •oW Rozdział :i. Rachunek różniczkowy funkcji jednej zmiennej Zadanie 3.18. Prosta ma ró
Pochodna funkcji jednej zmiennej (18) 7 ZkLf (^) fd ^ Xlr 7/xf“7 70 ■> 2k a, 2.U- 7 O -(5 -
37639 Pochodna funkcji jednej zmiennej (11) V (-ca.-^-G) -/--Ti (-KvM -,1 -la (-A -h,+ !x>j fM
CREWLENGTHWINGSPANHEIGHT WING AREA ASPECT RATIO 84 M (275 FT 7 IN) 88.4 M (290 FT O IN) 18
skanuj0012 (233) 28,96-1547. -23,76-1217 18,84-1007
skanuj0012 (233) 28,96-1547. -23,76-1217 18,84-1007
informatyka05 k /fl /ll /El ft l z? 1 /I i i ,..iT l T l /Ti /1 i /<ł t /I i if t /1 i if l /i .
45952 informatyka05 k /fl /ll /El ft l z? 1 /I i i ,..iT l T l /Ti /1 i /<ł t /I i if t /1 i if l
więcej podobnych podstron