2013 02 27";04;36

Ćwiczenie 8 '•/

WYZNACZANIE MODUŁU SPRĘŻYSTOŚCI POSTACIOWEJ G ^RZEZ POMIAR KĄTA SKRĘCENIA PRĘTA

A. PRZYPADEK PRĘTA O PRZEKROJU KOŁOWYM 8.1. WPROWADZENIE

W prącie pryzmatycznym obciążonym w dwóch płaszczyznach prostopadłych do jego os’ dwiema parami sił o tych samych wartościach momentów i

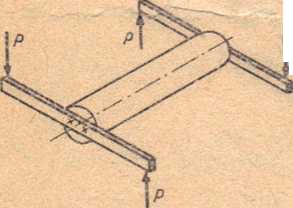
Rys. 8.1

przeciwnych zwrotach powstaje stan odkształcenia i naprężenia zw^rany czystym skręcaniem.

* Jeżeli gumewy pręt o przekroju kołowym, z na-ryso-waną na nim siatką składającą się z tworzących i okręgów kół prostopadłych do osi pręta, poddany zostanie czystemu skręcaniu, to będzie można zaobserwować, że:

-    oś pręta pozostanie po odkształceniu nadal linią prostą,

-    okręgi kół nie ulegają zniekształceniu, a powierzchnie czołowe pozostaną nadal płaskie,

-    promienie narysov'are na powierzchniach czołowych pozostaną po odkształceniu nadal liniami prostymi,

-    tworzące odchylą się od pierwotnego sw>ego położenia o pewien kąt y- , zwany kątem odkształcenia postaciow'ego,

-    powierzchnie c.zołow'e pręta obrócą się względem siebie o pewien kąt <f, zwany kątem skręcenia.

LNa podstawie tych spostrzeżeń można wnioskować, że wszystkie przekroje poprzeczne prętów o przekroju kołow'ym pozostają w trakcie skręcania płaskie, a promienie tych przekrojów pozostają liniami prostymi,. Jeżeli z pręta skręcanego momentem M_s wytniemy (dwiema- płaszczyznami prostopadłymi do osi pręta) walec o wysokości dx (patrz rys. 8.2b), to w-artość kąta odkształcenia postaciowego na powierzchni zewmętrznej jest róv;na

(8.1)

r ć(f> d x