badwłasn0021

42    -

Podobnie jak poprzednio dla wybranej płaszczyzny prostopadłej do jednej z osi, na ściankach tego prostopadłościanu znajdzie-my następujące składowe:

42    -

llltynika z tego, że stan naprężenia rozpatrywanego prostopadłościanu jest określony za pomocą trzech składowych normalnych

W najbardziej ogólnym przypadku naprężenia występujące na ściankach prostopadłościanu zależą od współrzędnych punktu, w którym ten prostopadłościan został przyjęty. Składowe stanu naprężenia są zatem pewnymi funkcjami współrzędnych w obranym układzie współrzędnych

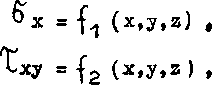
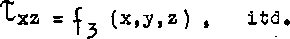
Jeśli założymy, że rozpatrywany^prostopadłościan znajduje się w równowadze, to muszą być spełnione warunki

2 Px .= o , 2Py = o ,

2Pz = o ,

2 Mx = 0 ,

zm = o ,

2MZ =    0 ,

Układając dla elementarnego prostopadłościanu warunki równowagi i przeprowadzając odpowiednie przekształcenia otrzymamy:

I Xxyl = 1 ^yxl

ItyzU (Tzyj, l zx I = I ^xz|,

z czego wynika, że stan naprężenia w punkcie jest jednoznacznie określony przez trzy składowe normalne i trzy składowe styczne

Przecinając ciało płaszczyzną łub kilkoma płaszczyznami (wyodrębniając prostopadłościan) można kierunek osi układu współrzędnych, a więc i kierunek zewnętrznej normalnej ustalić zgodnie z prostą działania naprężenia (oC = 0). Przy tak przyjętym układzie, stan naprężenia w danym punkcie jest określony jedynie składowymi normalnymi, gdyż składowe styczne X równe są zeru.

Składowymi tymi są;

^1, ^S2, 63 ,

określone jako naprężenia główne, naciągamy z tego bardzo ważny wniosek, że naprężeniu 6_n o wartości ekstremalnej 6 (Hys. 22 i 23) nie będzie towarzyszyć naprężenie styczne X= 0 . Ekstremalne naprężenie normalne jest jednocześnie naprężeniem całkowitym (wypadkowym) w rozpatrywanym przekroju, a w konsekwencji kierunek normalnej do tego przekroju pokryje się z kierunkiem samego naprężenia ekstremalnego.

Dla odróżnienia od kierunków dowolnych, osie układu współrzędnych, pokrywającego się z kierunkami głównymi, oraz naprężenia główne oznaczać będziemy wskaźnikami liczbowymi, odpowiadającymi oznaczeniu danego kierunku głównego.

Wartości naprężeń głównych, jak również kierunki główne, zależą tylko od sposobu obciążenia danego ciała i są one niezależne od wybranego układu współrzędnych. Wykorzystując pojęcie naprężenia głównego i uwzględniając zależności określające pierwiastki równania sekularnego, można naprężenie główne przedstawić w postaci

=	^6m ^+	2/3 6 H . COS oO ,
6^ =	^6m +	2/3 6h . cos(u? --120°),
63 =	^6m ^+	2/3 Gh . cos (u?- 240°),

gdzie ^ m,    i oj są niezmiennikami stanu naprężenia ( nie

zmienniki posiadają stałą wartość przy zmianie ukłaću odniesienia ) i wynoszą:

6.³

₊ 6₂ + 63    ₍

3

⁶h - -f¹ %-