BEZNA~35

Przyjmując = -ł; a₂ = — 1, otrzymujemy b_t = —3, b₂ = -2. Zatem wektory własne mają wartości

*--[=3

Macierz diagonalną D wyznaczamy wg następującej zależności:

D = P*AP

przy czym macierz P jest macierzą, której kolumnami są wektory własne macierzy A czyli P = [x_x x₂] oraz

D =

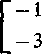
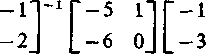
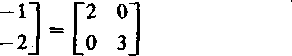
Funkcję macierzy e^A' obliczamy wg następującej zależności:

A t

Pe^DtP^_1

przy czym

Zatem

At

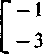
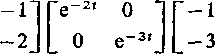
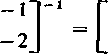
2e"^2t — 3e ^3t — e^-2,+e^-3t 6e^-2' —6e^-3'    —3e^-2f+2e^_3t

Poszukiwany wektor stanu

x =

e^o

2e^-2' —3e^-3* 6e^-2t-6e^_3t

—e ^2,+e~^3t -3e-^2,+2e-^3t

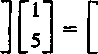
2e^_3‘—3e^_2,1 4e-³*-9e-^2,J

i_L = 2e^-3t —3e~²‘ A u_c = 4e~^3t—9e^_2t V

8.27.

Stosując metodę zmiennych stanu, obliczyć prąd w cewce oraz napięcie na kondensatorze w obwodzie przedstawionym na rys. 8.27, jeżeli w chwili Z = 0 zamknięto łącznik W.

Dane: i± = I_ź = 4 A; R = R_t = 1 £2; C = 0,5 F; L = 1 H.

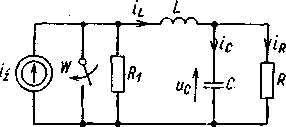
Rys. 8.27

233