skanuj0086 (40)

i 52___■    _ B. Cieślar

Przyjmując t = 9 cm, otrzymamy naprężenia, których wykresy pokazano na rys. 4.10.3b,c.

a

E    [g

y

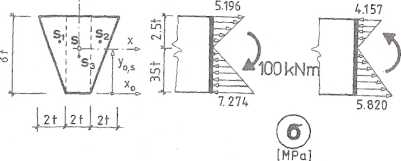
Rys. 4.10.3

80kNm

l 4.11. I Określić nośność żeliwnej belki wspornikowej o przekroju poprzecznym pokazanym na rys. 4.11.1. Dane: fdr = 150 MPa, fa = 600 MPa, I = 1,4 m.

		o
	-““I	e
	1	\j un in.
4-5--4 A	1.16 cm Jh

Rys. 4.11.1

Rozwiązanie

Wyznaczamy położenie środka masy przekroju w układzie osi x₀ ,y₀ {rys. 4.11.2). Ze względu na symetrię przekroju:

x₀s = 0;

= 17,05 cm.

20-30 15-18-15 12,5 ^y°^s~ 20-30-18-15

Obliczamy moment bezwładności względem osi x:

j_{x =} 20_|0l₊₂₀.₃₀₍2₎₀₅)2 JJM51₊₁₈.-i 5(4,55)² J = 36870 cm'

y, y_c

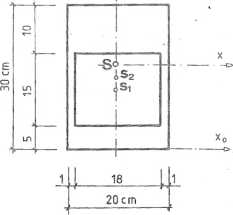
Rys. 4.11.2

5r< R_r

łJ

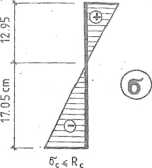
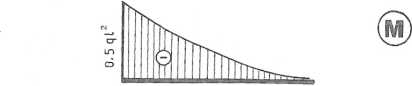
Rys. 4.11.3