69672 skanuj0087 (40)

154 B. Cieślar

Określenie dopuszczalnego obciążenia „q”: M_max = 0,5ql² = 0,98q (rys. 4.11.3).

(D

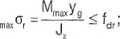
0,98q• 12,95 • 10~² 36870-10^-8    *

q < 0,4358 MN/m;

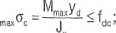
(2)

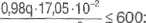
36870-10^-8 q< 1,3240 MN/m.

Z rozwiązania nierówności (1) i (2) wynika, iż obciążenie belki nie może przekroczyć wartości q = 435,8 kN/m.

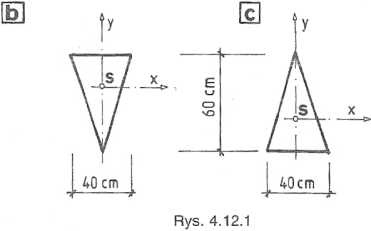
4.12. | Przekrój poprzeczny belki (rys. 4.12.1 a) ma kształt trójkąta równoramiennego i może być ułożony w dwóch pozycjach (rys. 4.12.1b,c). Przy którym ułożeniu przekroju belka będzie posiadać większą nośność? Czy w każdym przypadku ułożenia przekroju, tzw. przekrój niebezpieczny znajduje się w tym samym miejscu belki? Jako dane przyjąć: I = 12 m, f* = 60 MPa, fdc - 100 MPa.

Rozwiązanie

Wykresy sił wewnętrznych przedstawiono na rys. 4.12.2.

Obliczenie momentu bezwładności przekroju:

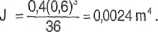
Z wykresu momentów zginających wynika, iż: największy moment dodatni - _maxM⁺ = 18q; największy moment ujemny - _raaxM' = 24q. Określenie nośności belki dla przekroju z rys. 4.12.1 b.

maxM⁺ = 18q;

M<_f •

0,0024    *' q < 0,020 MN/m;

18q 0,2 . . 0,0024 " ^dc’

q < 0,067 MN/m. maxM = 24q;

24q • 0,4 _f . 0,0024    *’

q ^ 0,025 MN/m;

24q0,2    .

0,0024 ^dr’

q < 0,030 MN/m.

s\\\W

jlTTTTT~m

1/3

W tym przypadku nośność belki wynosi 20 kN/m, a przekrój niebezpieczny to przekrój, w którym działa moment mniejszy lub równy 18q.

Określenie nośności belki dla przekroju z rys. 4.12.1 c. maxM ~ 18q;