21154 skanuj0042 (28)

64

B. Cieślar

N4 = *X= -0.375P;

N₅ = -X= -0.375P;

N = -X-2P= -2.375P. Wykresy - rys. 2.18.2a. Naprężenia normalne:

w    p

o, =~L=+1,8125^;

N    p

o₂=^= +0,3125

N    p

0₃    =-^=+0,6250

N    p

0₄    =-^-=-°,³⁷50

N    P

o_s = ^-=-0,1875^;

ł\L    P

^ae⁼ p ="1>1875 |t.

Wykresy-rys. 2.18.2b.

Przesunięcia punktów leżących na osi pręta:

u_a = ^=1.₈₁25_EF

Pa

u -24®₊itó. -2 125^ ^U° ” 2EF ⁺ 2EF ”^2,125 EF

Pa

u . N₂a N3a_₂₇₅l ^U°"2EF ⁺ 2EF⁺EF"^2,7 EF^!

N.a N₂a N₃a , N₄a ₀<r7_Pa. ₌^₌₊^_r+^-₊-^ =2,375^,

^un = 2e_f ⁺ 2EF

r+-Sdl=1,375||;

2EF 2EF

EF

Uk

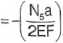
=1,1875||.

Wykresy - rys. 2.18.2c.

2.19. Jednorodny pręt stalowy obustronnie sztywno zamocowany (rys. 2.19.1) został równomiernie oziębiony o At na odcinku I = pi. Sporządzić wykres siły osiowej,

naprężeń normalnych oraz przemieszczeń przekrojów poprzecznych pręta. Obliczenia wykonać dla: At = -20°C, p = 0.6, a, = 1,15-10‘⁵, E = 2-10'⁵ MPa, F = 20 cm², I = 10 m.

Rozwiązanie

Strona statyczna

(1)

(2)

(3)

SP_z=0; V_A - V_B = 0; Strona geometryczna

Al=0, przy czym: Al = AI(N)+AI(At). Strona fizyczna

AI(At) = a_t Ath

m

I-

4

i^v-

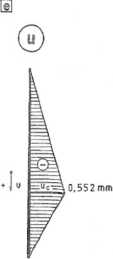
Rys. 2.19.1

Podstawiając (3) do (2) otrzymujemy:

U

EF

+ a_tAt-pi = 0; stąd: V_A = -pa_t AtEF;

V_A = -0,6-1,15-10'⁵ (-20)-2-10⁵-20-10⁴ =2,76-10‘³ MN; V_A iH 2,76 kN.

Siły osiowe:

N(Z!> = N(z₂) = V_A = 2,76 kN.

Naprężenia normalne w dowolnym przekroju: a= N ₌ .2,76-10^-3

F 20-10⁴

= 1,38 MPa.