skanuj0143 (10)

266 B. Cieślar

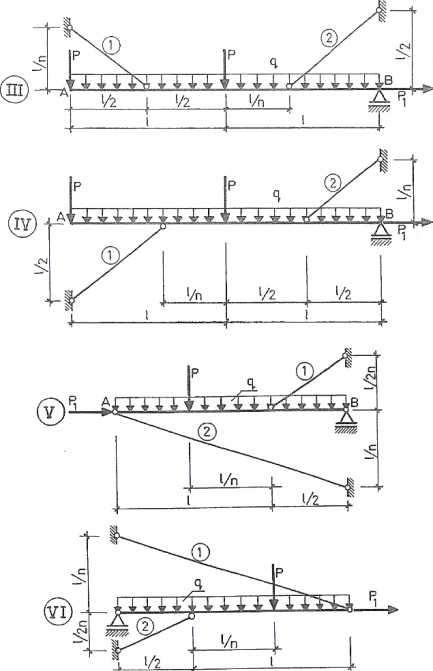
Rys. 6.28.3

VII. STAN NAPRĘŻENIA, STAN ODKSZTAŁCENIA

Podstawowe wzory, niezbędne do rozwiązywania zadań w tym rozdziale, podano w poprzednich rozdziałach. Jak już wspomniano o tym w rozdziale I, składowe stanu naprężenia i stanu odkształcenia są składowymi tensora o walencji 2. Składowe można zapisać w postaci macierzy:

dla stanu naprężenia:

To ⁼ by]

i dla stanu odkształcenia:

T« = [sy].

Niezmienniki obu stanów można zapisać stosując konwencję sumacyjną Einsteina. Mówi ona, iż w wyrażeniu, w którym wskaźniki powtarzają się, należy przeprowadzić sumowanie podług nich. Pokażemy to na przykładzie stanu naprężenia.

W poniższych wzorach sumowanie przeprowadzimy podług wskaźników i,j = 1,2,3.

51    = a_a = di + 022 ⁺ 0*33!

52    ⁼ ~2 bli °jj “ oy Ojj).

Po zsumowaniu podług „i” mamy:

S2 = 4 (011 Cjj + C22 Ojj ⁺ <733 Ojj - 01 j 0)1 - C2j ^CTj2 ■ °3j Oj3). a po zsumowaniu każdego składnika podług j" i uproszczeniu otrzymamy.

52    = 1 (dl 022 + 011 033 + 022 033 - 012 021 - 013 031 - 023 032):

53    = det [ad-

Powyższe składowe stanu naprężenia określono w kartezjańskim układzie współrzędnych Xi, X2, X3. Przy tradycyjnym oznaczeniu osi zachodzi odpowiedniość.

011 = o_x; 022⁼ o_y;    033 ⁼ o*;

012 = Txy; 023 ⁼ Ty_Z;    013 = *«•