skanuj0135 (10)

250 B. Cieślar

Aby w murze nie wystąpiły naprężenia rozciągające, linia obojętna nie może dzielić pizekroju na dwie części (rys. 6.12.1b), czyli:

|x| > 0,19, a stąd:    L < 0,8664m.

Określenie dopuszczalnej wysokości muru z warunków:

max

max

(D

(2)

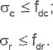
Z warunku (1) otrzymujemy:

6,84L10~³ O^-O/IS-IO"⁸ _1fi.

0,38    0,004573    ’ ’

0.020776L² + 0,018L - 1,8 ś 0;

L e (-9,336; 8,885).

Z warunku (2) otrzymujemy:

634L-10-³ 0,5L²-0,19-10"³ ^_n2.

0,38    0,004573

0.020776L² - 0,018L - 0,2 < 0;

L e (-2,700; 3,566).

Ponieważ interesuje nas rozwiązanie dla L > 0, to z nierówności (1) i (2) wynika, iż dopuszczalna wysokość muru wynosi Lmax³ 3,566 m. Należy tu przypomnieć, że dla L <, 0,8664 m w przekroju a - a nie wystąpią naprężenia rozciągające.

W rozwiązaniu nie sprawdzano stateczności muru.

W zadaniach 6.13 do 6.23 należy wyznaczyć rdzeń przekroju.

Tok postępowania przy wyznaczaniu rdzenia będzie następujący:

1)    wyznaczenie współrzędnych środka masy (x'_s,y'₈);

2)    obliczenie momentów bezwładności i momentu dewiacji względem osi centralnych (Xo, y₀);

3)    określenie położenia osi głównych, centralnych (x, y);

4)    obliczenie wartości głównych, centralnych momentów bezwładności i kwadratów promieni bezwładności;

5)    obliczenie współrzędnych wierzchołków konturu przekroju w układzie osi głównych, centralnych za pomocą wzorów:

x = Xo cosp + y₀ sinp, y = - Xo sinp + y₀ cosp,

VI. Zginanie z rozciąganiem (ściskaniem) osiowym... gdzie:

Xo, Yo - współrzędne wierzchołków w układzie (x₀, y₀), p - kąt odmierzany od osi x₀ do osi x przeciwnie do ruchu wskazówek zegara jako dodatni;

współrzędne wierzchołków konturu można również odmierzyć na rysunku przekroju wykonanego w odpowiedniej skali;

6) obliczenie, według wzorów (VI-4), współrzędnych punktów przecięcia się prostych ograniczających rdzeń z osiami x, y lub też wkreślenie tych prostych w inny, znany sposób.

Alternatywnie, za pomocą wzorów (Vł-3), można obliczyć współrzędne wierzchołków rdzenia.

Przedstawiony tok postępowania pokażemy na przykładzie zadania 6.13.

6.13.

Wyznaczyć rdzeń przekroju pokazanego na rys. 6.13.1.

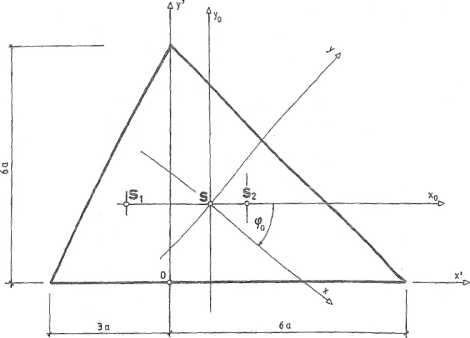
Rys. 6.13.1

Rozwiązanie

1. Obliczenie współrzędnych środka masy w układzie (x\ y¹).

W tym celu figurę dzielimy na dwie składowe o środkach w punktach Si i S2. Fi m 9a²;    F₂=18a²;    Si(-a;2a);    S2(2a;2a); F = 27a²;