skanuj0060 (10)

100 B. Cieślar

100 B. Cieślar

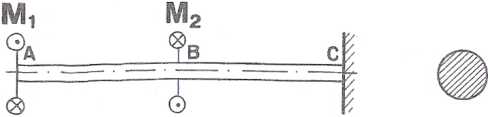
Pręt o przekroju kołowym (rys. 3.2.1) obciążono dwiema parami sił i M₂.

Jak duża była wartość momentu Mi, jeśli wiadomo, iż maksymalne naprężenie styczne na odcinku BC wyniosło 50 MPa, a M₂ = 10 kNm, d = 20 cm?

lii    d

----i--r    y.

Rys. 3.2.1

Rozwiązanie

Funkcje momentów skręcających (rys. 3.2.2a) Mi = -M,;

M = - Mt + M₂.

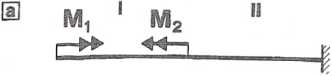
Rys. 3.2.2

III. Skręcanie_

101

Obliczenie momentu Mi:

Kl4    .₃

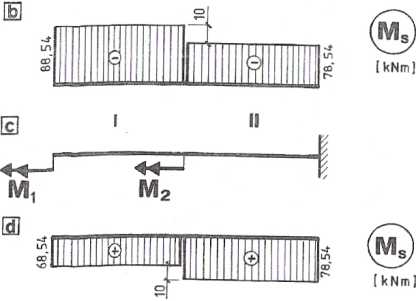
= 50; K| = 50^L; |M„| = 78,54 kNm.

JCu    16

32

|— M, +M₂| =78,58; =» -M,+M₂= 78,54 lub -(-M,+M₂) = 78,54.

Po rozwiązaniu otrzymujemy:

M-s = - 68,54 kNm lub Mi = + 88,54 kNm.

Tak więc, na odcinku BC naprężenia styczne równe 50 MPa można otrzymać dla dwóch wartości momentu Mi (rys. 3.2.b,d).

3.3.

Pręt o skokowo zmieniającej się średnicy (rys. 3.3.1) obciążono dwiema

parami sił Mi i M2. Jak duża powinna być wartość momentu M2, aby wytrzymałość obliczeniowa materiału była maksymalnie wykorzystana, jeżeli Mi =50 kNm?

m₂

	iii	G
—
A	—	0 <s>

oc-oi	ji-n
©
W	ki

Rys. 3.3.1

Rozwiązanie

Aby nośność materiału była w pełni wykorzystana, muszą być spełnione poniższe warunki:

<«x=V>    0)

-tr-łp    (2)

Powyższe warunki sprowadzić można do jednego warunku:

<³)

przy czym

Tl _ Kmax .		T3 K | II “d
^m8X wOJ *	oj d -	* 32
	2