skanuj0075 (10)

130___B. Cieślar

Przekrojem decydującym o doborze wymiarów (tzw. przekrojem niebezpiecznym) może być przekrój, w którym działa mniejszy (co do wartości bezwzględnej) moment zginający.

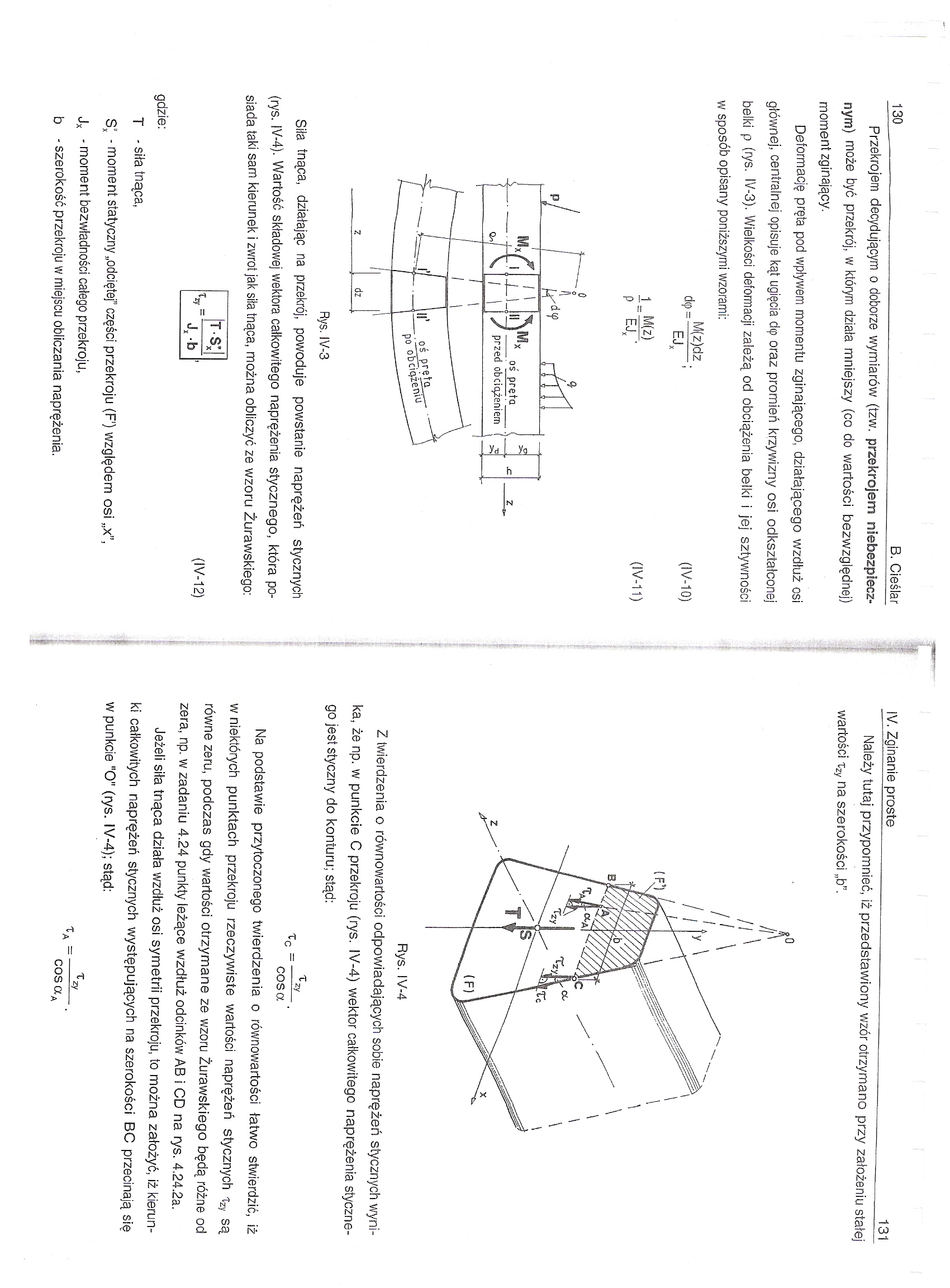
Deformację pręta pod wpływem momentu zginającego, działającego wzdłuż osi głównej, centralnej opisuje kąt ugięcia d<p oraz promień krzywizny osi odkształconej belki p (rys. IV-3). Wielkości deformacji zależą od obciążenia belki i jej sztywności w sposób opisany poniższymi wzorami:

dę=HE&;

EJ*

(IV-10)

i₌M p EJ_X ’

(IV-11)

Rys. IV-3

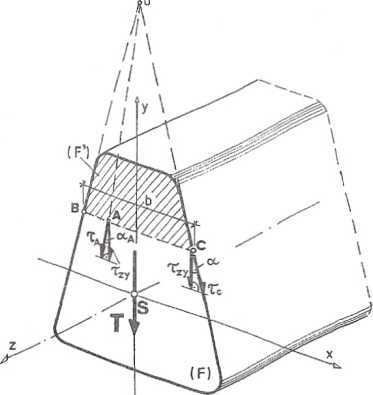
Siła tnąca, działając na przekrój, powoduje powstanie naprężeń stycznych (rys. IV-4). Wartość składowej wektora całkowitego naprężenia stycznego, która posiada taki sam kierunek i zwrot jak siła tnąca, można obliczyć ze wzoru Żurawskiego:

	t-s;|
	Jxb

(IV-12)

gdzie:

T - siła tnąca,

S’ - moment statyczny „odciętej" części przekroju (F) względem osi „x”, J_x - moment bezwładności całego przekroju, b - szerokość przekroju w miejscu obliczania naprężenia.

Należy tutaj przypomnieć, iż przedstawiony wzór otrzymano przy założeniu stałej wartości Tzy na szerokości „b”.

o

Rys. IV-4

Z twierdzenia o równowartości odpowiadających sobie naprężeń stycznych wynika, że np. w punkcie C przekroju (rys. IV-4) wektor całkowitego naprężenia stycznego jest styczny do konturu; stąd:

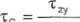
^c cos a

Na podstawie przytoczonego twierdzenia o równowartości łatwo stwierdzić, iż w niektórych punktach przekroju rzeczywiste wartości naprężeń stycznych są równe zeru, podczas gdy wartości otrzymane ze wzoru Żurawskiego będą różne od zera, np. w zadaniu 4.24 punkty leżące wzdłuż odcinków AB i CD na rys. 4.24.2a.

Jeżeli siła tnąca działa wzdłuż osi symetrii przekroju, to można założyć, iż kierunki całkowitych naprężeń stycznych występujących na szerokości BC przecinają się w punkcie "O" (rys. IV-4); stąd:

^A cosa_A