skanuj0132 (10)

244 B. Cieślar

krój pokazano na rys. 6.10.2. Naprężenie w dowolnym punkcie przekroju a - a obliczamy ze wzoru:

Mx

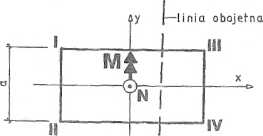
o(x,y) = |f

gdzie:

M = 0,5ql²-0,5-75-(4,8)² = 864 kNm; N = ql = 75-4,8 = 360 kN;

F = ab = 2b²,

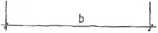
Rys. 6.10.2

Po podstawieniu otrzymamy:

-/y _V\ _ 360 • 10"³ 864-10~³ -x _

2b²    |b³

_ 180 • 10~³    1296-10"³ y

" b²    b⁴

Równanie linii obojętnej:

0 = 0; a stąd x = 0,1389b².

Linia obojętna jest, w tym przypadku, prostą równoległą do osi y i przecinającą dodatnią półoś x. Tak więc największe naprężenia wystąpią w punktach wzdłuż boku I - II przekroju (dla x = -a/2 = -b) i będą to naprężenia rozciągające. A zatem:

[180-10-³ 1296 10^_{r h}Ł_f .

I b²    b^4    ( 1^d’

0,180b +1,296 = 50b³;

50b³    -0,180b-1,296 = 0.

Obliczamy wartość lewej strony L(b) powyższej nierówności dla kolejno przyjmowanych wartości „b”. I tak:

L(0,5) = 4,864;

L(0,4) = 1,832;

L(0,2) = -,0932;

L(0,3) = 0,000.

Dla sprawdzenia obliczmy jeszcze wartość:

L(0,31) = -0,13775.

Tak więc

b ^ 30 cm jest szukanym rozwiązaniem dla b > 0. Dlatego można przyjąć:

b = 30 cm, a = 60 ćm.

Dla tak przyjętych wymiarów przekroju:

max^a= 50 MPa.

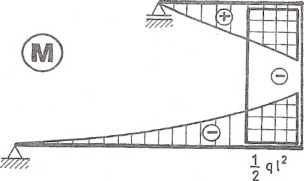
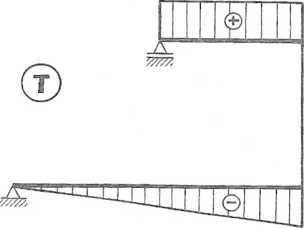
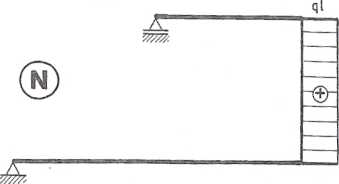
Rys. 6.10.3