scan 3 (8)

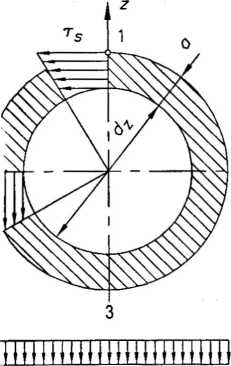
Przyjmujemy spoinę o grubości a — 5 mm. Przekrój oblicze-rowy spoiny, pokazany na rys. 3.10, ma kształt pierścienia o grubości o i średnicy wewnętrznej d_z.

+ <Jg

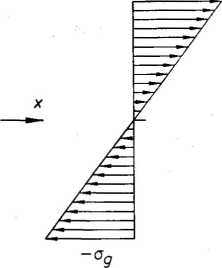
RYSUNEK 3.10. Przekrój obliczeniowy spoiny oraz naprężenia w spoinie

i

Naprężenia powstające w spoinie wskutek działania ciężaru G to:

—    naprężenia gnące a_g, osiągające największe wartości w punktach 1 i 3 na obwodzie zewnętrznym przekroju spoiny, o kierunku prostopadłym do przekroju obliczeniowego,

—    naprężenia skręcające t_s o największych wartościach na obwodzie zewnętrznym spoiny, o kierunku stycznym do tego obwodu,

—    naprężenia tnące r_t, o kierunku równoległym do kierunku działania ciężaru G — zakłada się, że naprężenia te są równomierne w całym przekroju.

Największe wytężenie występuje w punktach 1 i 3. Naprężenia w tych punktach są takie same co do wartości bezwzględnych. Wystarczające zatem będzie rozważanie jednego z nich, np. punktu 1.

Pole powierzchni przekroju obliczeniowego, wskaźnik wytrzymałości na zginanie oraz na skręcanie wynoszą odpowiednio:

^psp = \ [(d_z + 2a)² - dl] = ~ [(76 + 2 • 5)² - 76²] = = 1272 mm²

_w _ 2tt [(d_z + 2 a)⁴ -di] 2 • TT • [(76 + 2 • 5)⁴ - 7G⁴] ^x    64(d_z + 2a)    ~    64 • (76 + 2 ■ 5)

— 24359 mm³

2tr[(4 + 2a)⁴ - d⁴]    2 • tt ■ [(76 + 2 • 5)⁴ - 76⁴]

⁰ ~    32(d_z + 2a)    ~    32 • (76 + 2 • 5)

= 48 719 mm³

Momenty gnące i skręcające spoinę można wyrazić następująco:

M_g = Gl M_s = GR

Nie jest znana wartość ciężaru G, zatem naprężenia napiszmy jako funkcje ciężaru:

— naprężenia tnące

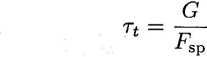
G

1272

MPa

— naprężenia skręcające

Ms	GR	G ■ 150	G
^Ts WQ	~ w0 '	48 719	324,79
naprężenia gnące
1 1 >*	Gl	G • 200	G
	~ Wx ^_	24 359	” 121,79

MPa

MPa

Traktując naprężenie skręcające jako działające wzdłuż długości spoiny (zawsze styczne do obwodu spoiny), można przyjąć, że kierunki występujących w spoinie naprężeń odpowiadają kierunkom oznaczonym na rys. 3.3. Dlatego zastosujemy do rozważanego przykładu warunek wytrzymałościowy (3.3) dla spoin pachwinowych

*V°g + ³(^rt² + ^Ts) < ^k

Dla zastosowanej stali k = 0,7 oraz

k = — = — = 204 MPa x_e 1,15

i«im