88573 skanuj0095 (28)

170 B. Cieślar

Sprawdzenie naprężeń:

214,64<fd = 215 MPa.

Oma*

W, = 139,42 + 25,38-4,2 = 246 cm³; NL, 52,8-10'

W, 246-10'

4.18. | Obliczyć niezbędną grubość „g” stalowych blach wzmacniających drewnianą belkę o prostokątnym przekroju poprzecznym (rys. 4.18.1), jeżeli: K = 32 kNm, q = 16 kN/m. f_d(d) = 15,5 MPa, f_d(s) = 190 MPa, E_d = 2-10⁴ MPa, E_s = 2-10⁵ MPa.

i-ii.....i-J-i

6.00

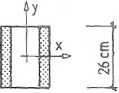
Rys. 4.18.1

Rozwiązanie

2 równań równowagi otrzymano:

Va - 32 kN; V_s = 64kN.

Wykresy sił wewnętrznych przedstawiono na rys. 4.18.2b,c.

Określenie niezbędnej grubości „g” blach stalowych.

W pierwszej kolejności musimy rozdzielić moment zginający, który działa na przekrój, na moment działający na część drewnianą (M_d) i na moment który działa na część stalową przekroju (M₃). Ponieważ sposób zamocowania blach do belki drewnianej zapewnia zgodność odkształceń, więc możemy napisać:

£d = £s,

lub

r<j = r_s,

£d i 8s - oznaczają odkształcenia liniowe w każdym punkcie belki na kierunku równoległym do jej osi, odpowiednio w części drewnianej i stalowej; r<j i r_s -sąpromieniami krzywizny osi odkształconej belki.

Wykorzystując drugi z przytoczonych warunków nierozdzielności przemieszczeń i na podstawie przytoczonego we wstępie do niniejszego rozdziału wzoru (IV-11)

j_{d =} 0_ł2(0|6)l _{= 2>}93,10. _m

12

możemy napisać:

(1)

gdzie:

= 2,93-10"³ g [m⁴];

g - grubość przykładki stalowej w (m).

Równocześnie całkowity moment zginający musi być równy sumie momentów działających na część drewnianą i stalową, więc:

M = M_d + M_s.    (2)

Rozwiązując układ równań (1) i (2) otrzymamy:

M    i,, M

1 +

Ł!l’

EJh

-tt

Podstawiając do powyższych wzorów największą wartość momentu zginającego, M = 128 kNm oraz obliczone wartości momentów bezwładności i podane wartości modułów Younga, otrzymamy:

M =■

128M

1+-

1

100g

Obliczenie największych naprężeń normalnych w obu częściach:

_d _ M_d -0,13 _ 128-1CT³ 0,13    _ 56,792 .

^max Jd (1+100g)2,93 • 10^-4 “ 1 +100g ’

M -0,13

128-10-³-0,13

5,6792

^Js ^¹ + iÓOg^)2,93 '¹⁰^^g 0,01 + 9

Obliczenie grubości blach przykładkowych z warunku wytrzymałości:

_<ax= 56^2 <15_i5 MPa; ^max 1 + 1 OOg    ’

g > 0,02664 m;

<190 MPa;

56,792

0,01+ g g > 0,01989 m.

Przyjęto g = 28 mm.