skanuj0113 (24)

206

B. Cieślar

Funkcja naprężeń:

(D

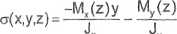
gdzie:

x, y - współrzędne punktu, w którym obliczamy naprężenie;

J_x = 3060cm⁴;

J_y = 162cm⁴.

Znak przed M_x(z) we wzorze (1) wynika ze zwrotu wektora M_x(z), który jest przeciwny do dodatniego zwrotu osi „x".

Ponieważ linia obojętna przechodzi przez tę ćwiartkę układu współrzędnych, w której znajduje się wektor momentu zginającego, to z jej położenia wynika, iż w każdym przekroju największe naprężenia wystąpią w punktach I i ii. Współrzędne tych punktów są następujące:

I - (0,5s;0,5h); II - (-0,5s;-0,5h),

gdzie: s = 9,8 cm (szerokość stopki dwuteownika), h = 22 cm (wysokość).

Jeżeli powyższe współrzędne podstawimy do wzoru (1), to obydwa składniki będą mieć znak (punkt I) lub (punkt II). Chcąc obliczyć największą wartość naprężenia wystarczyłoby znaleźć taki przekrój, w którym momenty M* i M_y osiągają największą wartość. Jak widać to z wykresów tych momentów, takiego przekroju w żadnym z dwóch przedziałów nie ma. Największe naprężenie wystąpi zatem na granicy obydwu przedziałów lub będzie to ekstremum wewnątrz przedziału BC. Jeżeli w przedziale BC będzie ekstremum a, to z fizycznego sensu zadania wynika, iż będzie to wartość największa. Przesuwając się wzdłuż belki, od miejsca wystąpienia ekstremum w kierunku podpory C, naprężenia muszą maleć (cc « 0).

Poszukujemy ekstremum funkcji o(z) w przedziale BC, dla punktu II przekroju,

gdyż KH4

, . (0,5qlz - 0,5qz²) • 0,5h 0,25Pz-0,5s

^wy

Warunek konieczny istnienia ekstremum funkcji:

dz

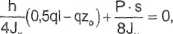
a stąd: z₀ = 2,84 m; z e (0;3).

V. Zginanie ukośne__

207

Tak więc:

[0,5 -10 • 10"³ • 4 -2,84 - 0,5 • 10 • 10“³(284)²] • 0.11

W    soeolo¹⁵-⁺

0,25 • 4 • 10"³«2,84 • 0,049 ⁺-162-10~⁸--= ^{146,114 MPa}

Największe naprężenie normalne w belce wynosi 145,114 MPa.

5.6,;- W przekroju poprzecznym pręta (rys. 5.6.1) działa moment zginający „M”. Określić jego wartość i położenie wiedząc, iź naprężenia w punktach I i II są równe: en = 100 MPa, on = -200 MPa.

Rozwiązanie

Moment M (rys. 5.6.1) rozkładamy na dwa składowe momenty wzdłuż osi x i y o wartościach równych odpowiednio M_x =Mcos<p i M_y = Msin<p. Wtedy funkcja naprężeń ma postać:

gdzie:

j_x =r ?P:³⁰-³ = 15000 cm⁴; 36

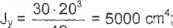
48

x, y - współrzędne punktu, w którym obliczamy o;

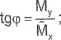
. My sintp = ~ M

Naprężenie w punkcie l-(-0,1; -0,1):

M_x(-0,1)    -My(-0'¹)__{= 100}

15000-10”⁸ 5000-10"⁸

(D

Naprężenie w punkcie ll-(0,T,-0,1):

15000-10^-8    5000-10

=-200.

(2)