skanuj0116 (24)

a

212_B. Cieślar

5.8.2. Obliczenie momentów zginających Mc,p ⁼ Vd-4 ⁼ K;

Mc,i = V_o-4-K = 0;

M_BiP = V_d-6 - K = 0.5K;

M_Bii = - Va-3 = 1.5K.

Wykres momentów zginających - rys. 5.8.2b.

Wykres siły poprzecznej - rys. 5.8.2c.

5.8.3 Wyznaczenie głównych, centralnych osi i momentów bezwładności (rys. 5.8.3) 5.8.3.1. Położenie środka masy w układzie x₀,y_0 w __ 2a²(-0,5a)+a²(-1,5a) _ 5„2

^y”--P--~6^a

Ze względu na symetrię: x₀=₊|_a.

5.8.3.2. Obliczenie centralnych momentów bezwładności

2aa³

12

aa~

12

+a"

2/4.

Ze względu na symetrię:

J -Ha^{4 j}/ - ₁₂^a ■

5.8.3.3, Położenie osi głównych, centralnych.

Ponieważ oś „x” jest osią symetrii, więc osie x,y są osiami głównymi, centralnymi.

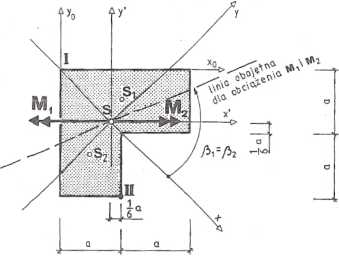
Rys. 5.8.3

5.8.3.4. Obliczenie wartości głównych, centralnych momentów bezwładności

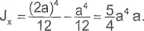
Ponieważ

Jx .Jy " Jy "T Jy¹, to stąd wynika:

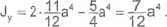
Dła a = 0,12 m mamy:

J_x = 2,592-ICrW; J_y = 1,2096-10"⁴ m⁴.

5.8.4. Obliczenie dopuszczalnej wartości K 5.8.4.1. Przekrój obciążony momentem dodatnim M = K Funkcja naprężeń M_xy M_yx

<*i= j *"“j    ¹

^Jx ^Jy

gdzie M_x = M_y = M J2/2 = K-^2/2.

Równanie linii obojętnej (o = 0):

M_xy M x

j ⁺-f-=^0:

x    y

y = 2,143 x;

tg Pi = 2,143, Pi = 65°.

Z położenia linii obojętnej wynika, iż największe naprężenia normalne wystąpią w punktach I i II przekroju, więc:

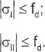
(D

(2)

Współrzędne punktów I i II wynoszą:

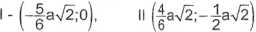
a wtedy warunki (1) i (2) przyjmują postać:

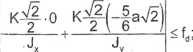
y

0,01875 MNm;

(1’)