skanuj0077 (29)

134__B. Cieślar

Największe naprężenia wystąpią (rys. 4.2.2c) w punkcie najbardziej odległym od osi obojętnej (x), a zatem w wierzchołku leżącym na osi symetrii. .

Korzystając ze wzoru (IV-6) mamy:

^j*^=-36 ^: y^⁼§^h=0’^08m;

<100,

⁰max^^fd;

0,2P-0,08 0,08-0,12³ 36

a stąd:

P< 0,048 MN.

A zatem dopuszczalna wartość sHy P wynosi 48 kN.

Rys. 4.2.2

|4.3. jj Jak duży powinien być parametr „a” przekroju poprzecznego belki pokazanej na rys. 4.3.1, aby belka posiadała odpowiednią nośność? W obliczeniach przyjąć: P = 100 kN, q = 25 kN/m, f_dr = 50 MPa, f* = 150 MPa.

g-oc

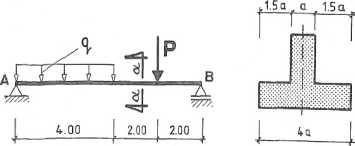
Rys. 4.3.1

IV. Zginanie proste__135

Rozwiązanie

4.3.1.    Wyznaczenie położenia środka masy (rys. 4.3.2d) w układzie współrzędnych xy.

Ponieważ przekrój posiada oś symetrii, to na niej znajduje się środek masy. A zatem:

x©s⁼ Oj

_ F₁y₁ + F₂y₂ 4a² • 0,5a + 2a² • 2a ^y“ F    6a²

4.3.2.    Obliczenie momentu bezwładności względem osi głównej, centralnej „X”:

J_x = ^4a^³ +4a²(0,5a)² + ^a^³ +2a²(a)² = 4a\

4.3.3.    Oddziaływania podpór (rys. 4.3.2a):

IM_a=°;    q-4-2+P-6-V_b -8 = 0;

£M_b=0;    -q-4-6-P-2-V_a -8=0;

stąd:

V_A = 100 kN; V_B= 100 kN.

4.3.4.    Siły wewnętrzne Przedział I z e (0;4)

M(z)= V z - 0,5qz² = 100z - 12,5z²;

M(0)= 0; M(4)= 200 kNm;

T(z)= V_A - qz= 100 - 25z;

T(0)= 100 kN; T(4)= 0; M_max = M(4).

Przedział II z e (2;4)

M(z)= V z - P(z-2)= 100z -100(z-2);

M(2)= 200 kNm; M(4)= 200 kNm;

T(z)= -V_B + P= 0.

Przedział III ze (0;2)

M(z)= Vb z= 100z;

M(0)= 0; M(2)= 200 kNm;

T(z)= -V_B = -100 kN.

Wykresy funkcji pokazano na rys. 4.3.2b,c.