72723 skanuj0057 (13)

94 B. Cieślar

Największe naprężenia styczne występują w punktach leżących w połowie dłuższych boków prostokąta i obliczamy je za pomocą wzoru:

gdzie:

W₀ = ab²h, tzw. zastępczy wskaźnik skręcania, b - długość krótszego boku prostokąta, h - długość dłuższego boku prostokąta, a - współczynnik zależny od h/b, wg tabeli IMA.

Maksymalne naprężenia styczne w połowie krótszego boku obliczamy za pomocą wzoru:

^ma^YW    iPfl

gdzie y jest współczynnikiem, wg tabeli IIIA.

Tabela IIIA

h/b	1,0	1,2	1,4	1,6	1,8	2,0	2,5	3,0	4,0	6,0	8,0	>10
a	0,208	0,219	0,228	0,234	0,240	0,246	0,258	0,267	0,282	0,299	0,307	0,333
P	0,140	0,166	0,187	0,204	0,217	0,229	0,249	0,263	0,281	0,299	0,307	0,333
Y	1,000	0,932	0,865	0,845	0,821	0,796	0,774	0,753	0,745	0,743	0,742	0,742

Wzajemny kąt obrotu dwóch przekrojów, odległych od siebie o „I”, przy założeniu, iż Mj/GJo jest stałe, obliczamy ze wzoru:

iJfft    OH-12)

^GJ0

gdzie:

J₀ = pb² h,

p - współczynnik, wg tabeli IIIA.

III.3. SWOBODNE SKRĘCANIE PRĘTÓW CIENKOŚCIENNYCH

Cechą charakterystyczną przekrojów prętów cienkościennych jest mała grubość ścianki przekroju (8|) w porównaniu do długości jego konturu (rys. III-5).

Pręty cienkościenne dzielimy na:

-    pręty o przekroju otwartym (rys. Ill-5a, b, c, d),

-    pręty o przekroju zamkniętym (rys. Ill-5e, f, g).

tu

E

t-r

et —

m

S

m

Ul

Rys. II1-5

111.3.1. PRĘTY O PRZEKROJU OTWARTYM

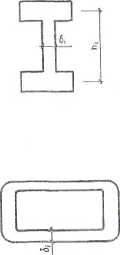
Jeżeli przekrój poprzeczny pręta ma kształt otwarty (rys. III-6) i składa się z długich, a cienkich prostokątów lub można go, z wystarczającą dokładnością zastąpić prostokątami (dwuteowniki, ceowniki itd.), to moment bezwładności możemy obliczyć za pomocą wzoru:

_r fw*

gdzie

bj, hi - długości odpowiednio krótszych i dłuższych boków prostokątów, na które można rozłożyć przekrój.

Współczynnik r\ zależy od rodzaju przekroju i dla kształtowników walcowanych przyjmuje wartości:

kątownik-r| = 1,10, dwuteownik - r| = 1,20, ceownik -r\= 1,12, teownik - r\ = 1,15.

Dla przekrojów złożonych z prostokątów można przyjąć rj = 1,0.

Największe naprężenia styczne występują w połowie dłuższego boku prostokąta o największej grubości bmax. a ich wartość obliczamy ze wzoru: