skanuj0146 (13)

272___B. Cieślar

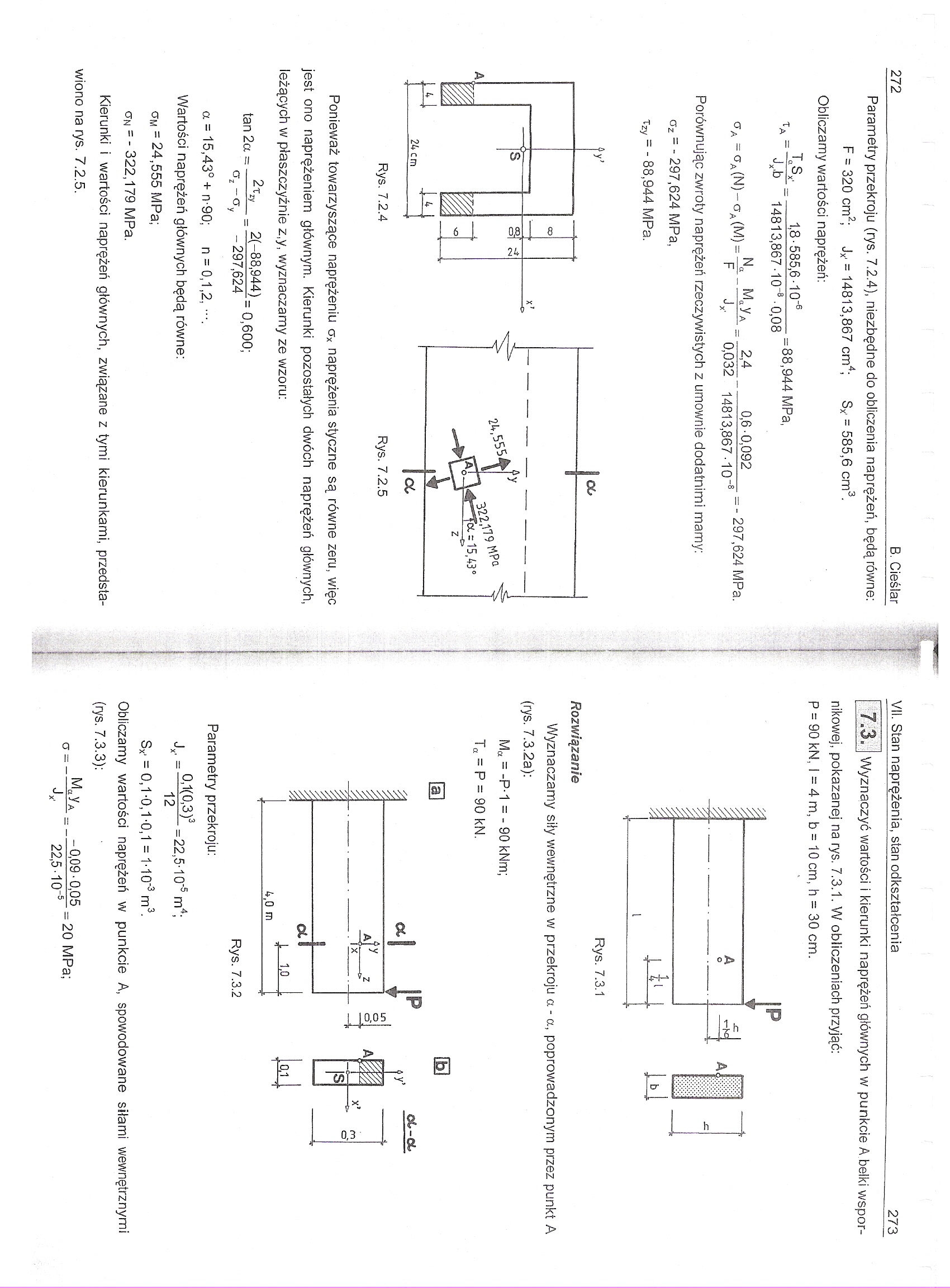
Parametry przekroju (rys. 7.2.4), niezbędne do obliczenia naprężeń, będą równe: F = 320 cm²; J_X' = 14813,867 cm⁴; S_x- = 585,6 cm³.

Obliczamy wartości naprężeń:

T„S_V.

1,8- 585,6 -10~'

J_x.b 14813,867-10"⁸-0,08

=88,944 MPa,

= -297,624 MPa.

rr = /—    (MY.^N°    ²'⁴    0.6-0.092

^A °a(N)    _a( ) _F    j ₀₀32 14813,867-10~⁸

Porównując zwroty naprężeń rzeczywistych z umownie dodatnimi mamy:

o_z = - 297,624 MPa, Tzy = - 88,944 MPa.

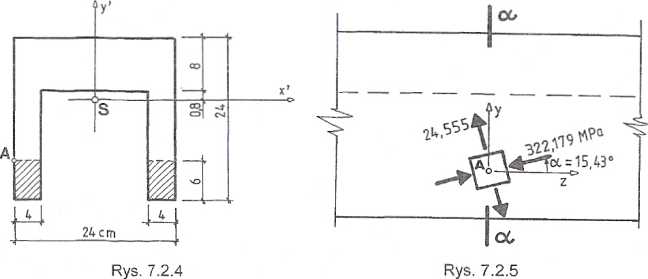
Ponieważ towarzyszące naprężeniu a_x naprężenia styczne są równe zeru, więc jest ono naprężeniem głównym. Kierunki pozostałych dwóch naprężeń głównych, leżących w płaszczyźnie z,y, wyznaczamy ze wzoru:

tan 2ct =

2x

kdglgffff- 0.600;

-297,624

a = 15,43° + n-90; n = 0,1,2,

Wartości naprężeń głównych będą równe: gm = 24,555 MPa;

gn = -322,179 MPa.

Kierunki i wartości naprężeń głównych, związane z tymi kierunkami, przedstawiono na rys. 7.2.5.

Wyznaczyć wartości i kierunki naprężeń głównych w punkcie A belki wspor

7.3.

nikowej, pokazanej na rys. 7.3.1. W obliczeniach przyjąć: P = 90 kN, I = 4 m, b = 10 cm, h = 30 cm.

Rozwiązanie

Wyznaczamy siły wewnętrzne w przekroju a - a, poprowadzonym przez punkt A (rys. 7.3.2a):

M_a = -P-1 =-90 kNm;

T_a = P = 90 kN.

E

OC-OC

fy’

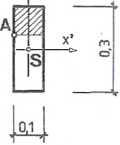
Parametry przekroju:

j,₌ml₌22,₆.io-=m-

S* = 0,1-0,1-0,1 = 1-10'³m³.

Obliczamy wartości naprężeń w punkcie A, spowodowane siłami wewnętrznymi (rys. 7.3.3):

<j = —

M_ay_A _

-0,09 0,05 22,5-10^-5

= 20 MPa;