skanuj0084 (30)

148

B. Cieślar

| 4.9. ?j Zaprojektować przekrój poprzeczny belki (rys. 4.9.1) złożony z dwóch dwu-teowników, jeżeli: Pt = 130 kN, P₂ = 40 kN, q = 10 kN/m, U = 215 MPa.

			i*	Ej
. i i	r		M i	1 (- J	SM
i			i<*		7Z&
	...	4.00		4.00 l
	10.00n			. J

Rys. 4.9.1

oircL

II

2 I NP

Rozwiązanie

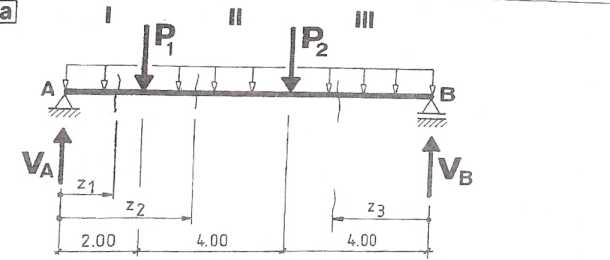
4.9.1.    Z równań równowagi otrzymujemy V_A = 170 kN;

V_B=100 kN.

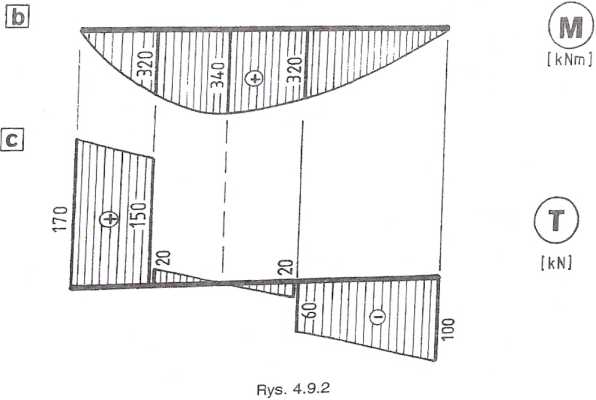
4.9.2.    Funkcje sił wewnętrznych (rys. 4.9.2a)

Przedział I - z e (0;2),

M(z) = V_A z - Q,5ap? = 170z- 5Z²;

M(0) = 0; M(2) = 320 kNm;

T(z) = V_A - qz = 170 - 10z;

T(0) = 170 kN; T(2) = 150kN.

Przedział II - z e (2;6),

M(z) = V_A z - 0,5qz² - Pi (z - 2) = -5z + 40z + 260;

M(2) = 320 kNm; M(6) = 320 kNm;

T(z) = V_A -qz - Pi = 40 - 10z;

T(2) = 20 kN; T(6) = -20kN.

Łatwo zauważyć, iż T(4)=. 0, a to oznacza, że funkcja M(z) ma w tym miejscu ekstremum. Obliczamy wartość M_Skstr-‘

M(4) = M_ei<_s,r = 340 kNm.

Przedział III - z e (0;4),

M(z) = V_B z - 0,5qz² = 100z- 5Z²;

M(0) = 0; M(4) = 320 kNm;

T(z) = -V_B + qz = -100 + 10z;

T(0) = -100 kN; T(4) = -60 kN.

340 kNm;

IV. Zginanie proste

149

4.9.3. Projektowanie przekroju

Z wykresu momentów zginających (rys. 4.9.2b) odczytujemy a zatem:

_ Mmax < f ■ O = -TT.— - d >

W_v

W_v >

M,

340 10 ^ ^ 581,4 cm²

215