43976 skanuj0126 (12)

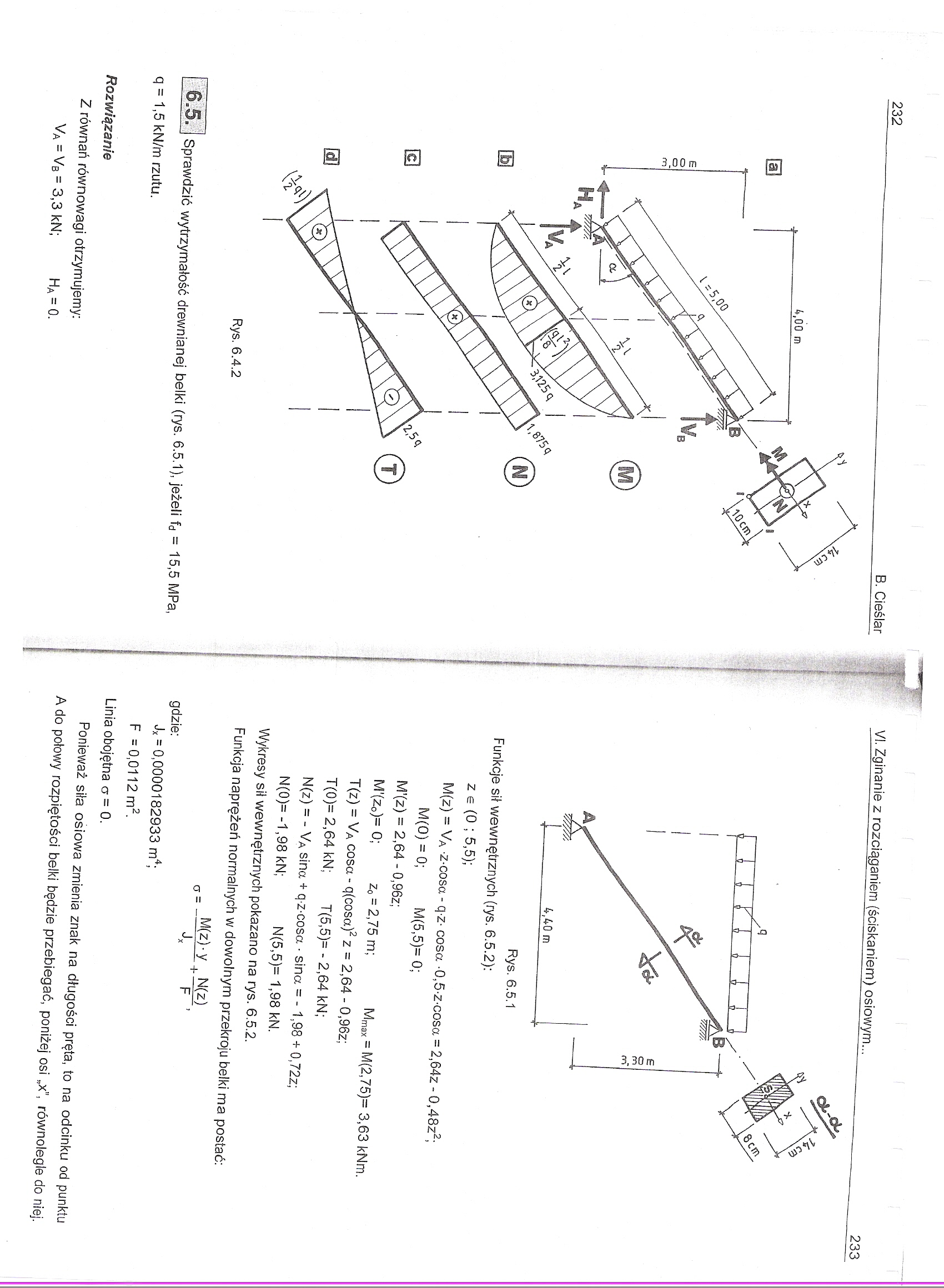
232 8. Cieślar

6:5;

Sprawdzić wytrzymałość drewnianej belki (rys. 6.5.1), jeżeli fd

15,5 MPa,

q = 1,5 kN/m rzutu.

Rozwiązanie

Z równań równowagi otrzymujemy: Va = V_B = 3,3 kN; H_A = 0.

Rys. 6.5.1

Funkcje sił wewnętrznych (rys. 6.5.2): z e (O ; 5,5);

M(z) — Va z-cosa - qz- cosa 0,5-zcosa = 2,64z - 0,48z²;

M(O) = O; M(5,5)= O;

M’(z) = 2,64 - 0,96z;

M'(Zo)= O; Zo = 2,75 m;    M_max = M(2,75)= 3,63 kNm.

T(z) = Va cosa - q(cosa)² z = 2,64 - 0,96z;

T(0)= 2,64 kN; T(5,5)= - 2,64 kN;

N(z) = - Vą sina + q z cosa • sina = - 1,98 + 0,72z;

N(0)= -1,98 kN;    N(5,5)= 1,98 kN.

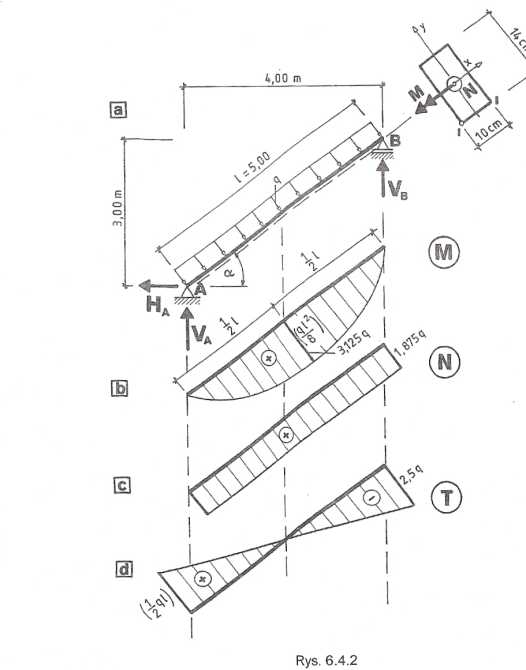
Wykresy sił wewnętrznych pokazano na rys. 6.5.2.

Funkcja naprężeń normalnych w dowolnym przekroju belki ma postać:

M(z)y N(z)

J_x F ’

gdzie:

J_x = 0,0000182933 m⁴;

F =0,0112 m².

Linia obojętna <s = 0.

Ponieważ siła osiowa zmienia znak na długości pręta, to na odcinku od punktu A do połowy rozpiętości belki będzie przebiegać, poniżej osi pc”, równolegle do niej.