79130 skanuj0125 (12)

230

6. Cieślar

Rozwiązanie

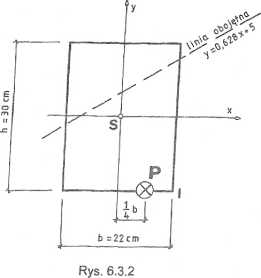
Dowolny przekrój poprzeczny a - a pręta jest mimośrodowo ściskany siłą P (rys. 6.3.2). Naprężenie w dowolnym punkcie przekroju obliczamy ze wzoru (VI - 2), w którym:

N = - P = -150 kN;

F = bh = 660 cm²;

Xp = 0,25b = 5,5 cm; yp = -0,5h = -15 cm; i_x² = 75 cm²; i_y² = 40,33 cm².

Tak więc:

_g_ -0,150L    5,5x    (—15)y~|

0,066 [_ 40.33    75 J’

gdzie x, y podstawiamy w [cmj.

Równanie linii obojętnej:

a * 0;    y = 0,682 x + 5,

gdzie x, y w [cm].

Z położenia linii obojętnej na przekroju wynika, iż największe naprężenie będzie w punkcie I, o współrzędnych (11 cm; -15 cm):

- __-0,150r, 5,5-11 , (-15)(-15)1.

¹ "Óro“66”[ 40,33    75 J*

a, = -12,5 MPa;

|a,)= 12,5 MPa <fd -15 MPa,

a zatem naprężenia nie są przekroczone w żadnym punkcie przekroju.

6.4.

Określić dopuszczalne obciążenie „q” drewnianej belki przedstawionej na

rys. 6.4.1, jeżeli fd = 13 MPa.

VI. Zginanie z rozciąganiem (ściskaniem) osiowym... Rozwiązanie

231

Równania równowagi:

2X =0; V_B -4 +q-5-2,5 =0;

P_z = 0;    -H + q-5sina = 0;

£M_s =0;    V_A- 4 + H_a • 3 - q 5-2,5=0.

Stąd dla sina = 0,6 otrzymujemy:

Vb = 3,125q; H_A = 3q;

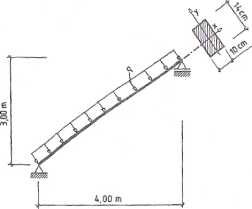
Rys. 6.4.1

V_A = 0,875q.

Obliczając charakterystyczne wartości sił wewnętrznych otrzymujemy wykresy rozkładu sił wewnętrznych, przedstawione na rys. 6.4.2.

Naprężenie w dowolnym punkcie przekroju (rys. 6.4.2a):

/    \ My N

Linia obojętna:

HU

^y= MF ‘

Określenie dopuszczalnego obciążenia belki, spełniającego warunek:

max⁰ —    ’

Z wykresów sił wewnętrznych wynika, iż przekrojem niebezpiecznym jest przekrój znajdujący się w połowie rozpiętości belki, w którym:

M = 3,125q oraz N = 1,875q.

Największe naprężenia normalne wystąpią wzdłuż boku I -1 przekroju, czyli dla y = - 0,07 m (linia obojętna przebiega równolegle do osi x, powyżej niej), a zatem:

3,125q 0,07 _j 1,875q ^

0,1(0,14)^{3 +} 0,1 0,14 12

stąd:

q< 0,00134 MN/m.

Dopuszczalne obciążenie „q” belki wynosi więc 1,34 kN/m.