skanuj0122 (12)

224 B. Cieślar

W przypadku gdy kontur przekroju ma kształt wieloboku, wygodniej jest wyznaczać proste ograniczające rdzeń. Zakładając w wierzchołkach konturu przekroju naprężenia równe zeru (lecz tylko w tym wierzchołku, przez który można poprowadzić co najmniej jedną prostą niedzielącą przekroju na dwie części - punkty I, II, -, K na rys. VI-3) otrzymujemy równania prostych, których fragmenty (odcinki AB, BC, CD, DE, EF, FA) wyznaczają rdzeń. Współrzędne punktów przecięcia się tych prostych z osiami x, y obliczamy ze wzorów:

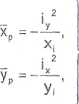
gdzie

i =!, II,.... K.

Rys. VI -3

Przyłożonej w punkcie A sile P odpowiada linia obojętna oznaczona literą „a” na rys.VI-3. Kolejnym punktom przyłożenia siły P, tzn. Ai, A2, —, A_n, B, odpowiadają linie obojętne oznaczone kolejno a-i, a2, a_n, b.

Przesuwając siłę P od punktu A w kierunku środka masy linia obojętna będzie odsuwać się od przekroju. Jeżeli siła P znajdzie się w środku masy, będzie to przypadek osiowego rozciągania (ściskania), a linia obojętna „ucieknie” do nieskończoności. Z kolei, przesuwając siłę P z punktu A w kierunku przeciwnym, linia obojętna zajmie położenie dzielące przekrój na część rozciąganą i ściskaną.

Na rys. VI - 3 rdzeń jest sześciobokiem ABCDEF.

VI. Zginanie z rozciąganiem (ściskaniem) osiowym... ZADANIA

mm

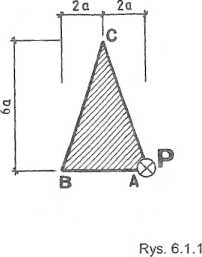
Zaprojektować trójkątny przekrój poprzeczny słupa

obciążonego w punkcie

A siłą mimośrodowo ściskającą P (rys. 6.1.1). Określić położenie linii obojętnej i sporządzić wykres naprężeń normalnych. Dane: P = 120 kN, f<i = 15 MPa.

Rozwiązanie

Funkcja naprężeń:

gdzie:

x, y - współrzędne punktu, w którym obliczamy naprężenia, Xp § 2a, yp = - 2a,

N = - P ponieważ siła jest skierowana do przekroju.

Obliczenie momentów i promieni bezwładności

J_x

4a(6a)²

36

24a

^Jy

_ 6a(4a)³ _ _{r 4}. --48    ⁸³ ’

i

F

24a⁴

12a²

= 2a

2.

i ²

'y

i ₌ _8il=2_a2 F 12a² 3^d