skanuj0147 (12)

274

B. Cieślar

.. T_aS_x. 0,09 •1-1CT

- = ,4 MPa.

J_x.b 22,5-10^-5 0,1 W przyjętym układzie współrzędnych składowe stanu naprężenia (rys. 7.3.2a) będą równe:

<j_x = Oy = Txy = Txz ⁼ O; cj₂ - 20 MPa; x₂y = — 4 MPa.

Ot

<3* !

ot

Rys. 7.3.3

Kierunki naprężeń głównych:

2tzv

tan 2a=-— =

2M)

20

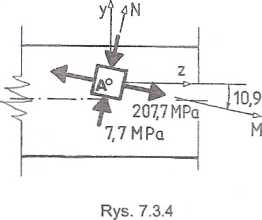
= -0,400;

a = - 10,9° + n-90.

Wartości naprężeń głównych:

o_M = 27,7 MPa; a_N *-7,7 MPa.

Ostatecznie:

ai = 27,7 MPa; 02 = o_x = 0;    <73 = -7,7 MPa.

Wyniki pokazano na rys. 7.3.4.

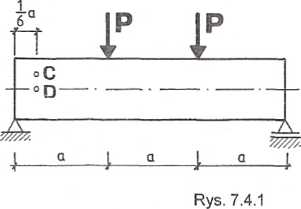
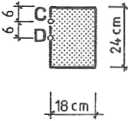
Belka o prostokątnym przekroju poprzecznym (rys. 7.4.1) jest obciążona

dwiema siłami P. W punktach C i D wyznaczyć wartości i kierunki naprężeń głównych. Dane: P = 60 kN, a = 2 m.

VII. Stan naprężenia, stan odkształcenia Rozwiązanie

275

Po wyznaczeniu reakcji podpór obliczono siły wewnętrzne w przekroju a - a (rys. 7.4.2a):

M_a = 20 kNm, T„ = 60 kN.

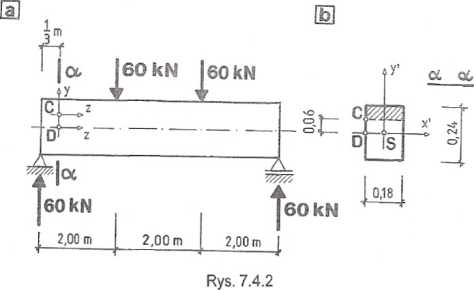
Parametry przekroju potrzebne do obliczenia naprężeń (rys. 7.4.2b): J_x. = ^0,18^²⁴^ = 20736 lO^m⁴;

Sj = 0,18 • 0,06 ■ 0,09 = 972-1 O^m³;

F = 0,18-0,24 = 432-10"⁴ m².

Obliczamy wartości naprężeń w punktach C i D przekroju a - a (rys. 7.4.3):

= 5,7870 MPa;

■6

= 1,5625 MPa;

_M_ay_c _ 0,02-0,06

20736-10'⁸ 0,06-972-10

J_x b    20736 -10^-8 -0,18

od - 0;

Tq =1,5-p- = 1,5—^°⁶ . = 2,0833 MPa.

⁰ F 432 ■ 10^-4

Składowe stanu naprężenia, różne od zera w punktach C i D, w przyjętym układzie współrzędnych (rys. 7.4.2a) będą równe:

- w punkcie C:

ct_z = - 5,7870 MPa;

Tzy = - 1,5625 MPa,