50127 skanuj0152 (12)

284 B. Cieślar

Ze związków fizycznych wyznaczamy pozostałe składowe stanu naprężenia:

^£y =jĘ-[⁰y-(^CTx⁺⁰z];

⁸z=^k-(o_x+o_y];

y mb ■

^G=    -■='8'¹⁰⁴'^MP»-

Po przekształceniu otrzymamy:

°y⁼T~5<⁸y ^{+ v8}*^): o_z=^~(s_z+^ve_y)^;

Tzy — G*Yzy-

Podstawiając dane liczbowe otrzymamy: o_z = 16,36 MPa; o_y = - 30,57 MPa; Tzy = 29,536 MPa. Kierunki naprężeń głównych:

=1,258;

tan 2a m

o₂-o_y

2-29,536 16,36-(-30,57)

a = 25,76° + n-90°.

Wartości naprężeń głównych, odpowiadające tym osiom, są równe: om = 30,62 MPa; on = - 44,83 MPa.

Komplet naprężeń głównych jest następujący:

01 = om = 30,62 MPa; 02 = o_x = I Odkształcenie liniowe na kierunku osi

®x f||J%    ⁺°z]⁼ - = 0,178-11

1;    03 = on = -44,83 MPa.

f obliczamy z równania fizycznego:

r⁴.

Odkształcenia główne są więc równe: si = 2.09110^-4;    82 = 0,178-10⁴;

s₃ = - 2,624-10-⁴.

Na podstawie obliczonych wartości naprężeń głównych i odkształceń głównych możemy stwierdzić, iż płaskiemu stanowi naprężenia w punkcie A towarzyszy przestrzenny stan odkształcenia.

VII. Stan naprężenia, stan odkształcenia_ 285

Wyznaczone kierunki naprężeń i odkształceń głównych pokazano na rys. 7.6.3. Z rysunku widać, że kierunki, w obydwóch przypadkach, pokrywają się ze sobą.

7.7.

Dla przedstawionych na rys. 7.7.1(a-f) rzeczywistych wartości i zwrotów

naprężeń wyznaczyć wartości i kierunki naprężeń głównych.

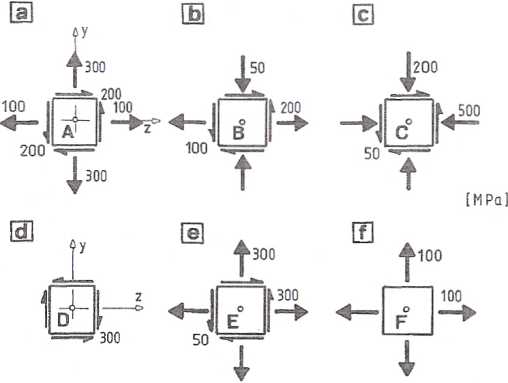
Rys. 7.7.1

Ponieważ z założenia cj_x = txy = Txz = 0, więc kierunki pozostałych dwóch naprężeń głównych określa kąt a, wyznaczony z poniższego wzoru:

tan 2a = —, a₂-a_y

a wartości naprężeń głównych, które tym osiom odpowiadają obliczamy za pomocą wzoru:

<*m =ik^+a»^±V^(a*'"^CTy>^+4xi]-

N *

Punkt A

c_z- 100 MPa; o_y = 300 MPa; xzy - 200 MPa;

2 200 _ ₀. ^tan2a- 100 - 300 ~^2,

a = - 31,72° + n-90°; gdzie n = 0,1,2,...;

ctm = 423,61 MPa; cr_N = - 23,61 MPa.