skanuj0156 (11)

292 B. Cieślar

Rys. 7.12.2

Rozwiązanie

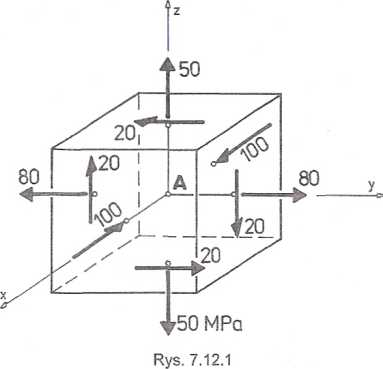
Składowe stanu naprężenia przedstawiono na rys. 7.12.1.

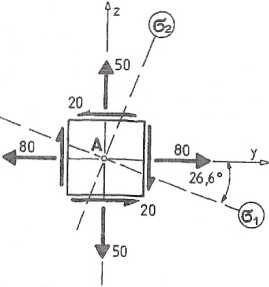
Ponieważ towarzyszące naprężeniu normalnemu a* naprężenia styczne są równe zeru, jest więc ono naprężeniem głównym. Pozostałe dwa kierunki naprężeń głównych leżą w płaszczyźnie osi y,z (rys. 7.12.2), a wartości tych naprężeń możemy obliczyć ze wzoru:

<*M = 2 [°z +    ± V(°z-°y)²⁺⁴V}

Podstawiając wartości liczbowe otrzymamy: om = 90 MPa; ctn = 40 MPa.

Wartości naprężeń głównych są zatem równe: ai = 90 MPa;

02    = 40 MPa;

03    = -100 MPa,

czyli w tym punkcie mamy przestrzenny stan naprężenia.

Dla zadanych, składowych stanu naprężenia w punkcie wyznaczyć warto

7.13.

ści i kierunki naprężeń głównych. Dane: txh = %z = 0, o_x = 60 MPa, cr_y = 60 MPa, a_z — 0, x_Xy⁼ 60 MPa.

Rozwiązanie

Łatwo zauważyć, iż towarzyszące o_z naprężenia styczne są równe zeru, czyli jest to naprężenie główne. Pozostałe dwa naprężenia główne leżą w płaszczyźnie osi x,y. Ich położenie określa kąt a, wyznaczony ze wzoru:

tg 2a =

^ _ 2 -60^3 _

60 -(-60)

a = 30° + n-90°.

Na rys. 7.13.1 pokazano kierunki naprężeń głównych.

Wartości naprężeń głównych są pierwiastkami równania wiekowego. Niezmienni

ki stanu naprężenia są równe:

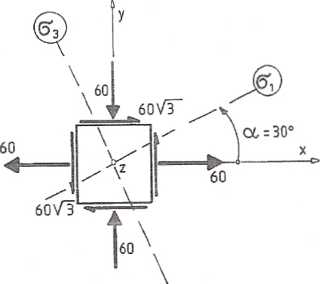
Rys. 7.13.1

51    =0,

5₂    = 14400,

5₃    = 0.

Równanie wiekowe przyjmuje postać:

a³ - 14400cr = 0;

©(o² -14400) = 0.

Z rozwiązania otrzymujemy: oi =0, on = 120 MPa, ctiii = -120MPa.

Naprężenia główne, ułożone w kolejności od największego do najmniejszego, wynoszą:

CTi = 120MPa, g₂ = 0,    03 = -120 MPa.

Jest to zatem przypadek płaskiego stanu naprężenia.