skanuj0123 (11)

226 B. Cieślar

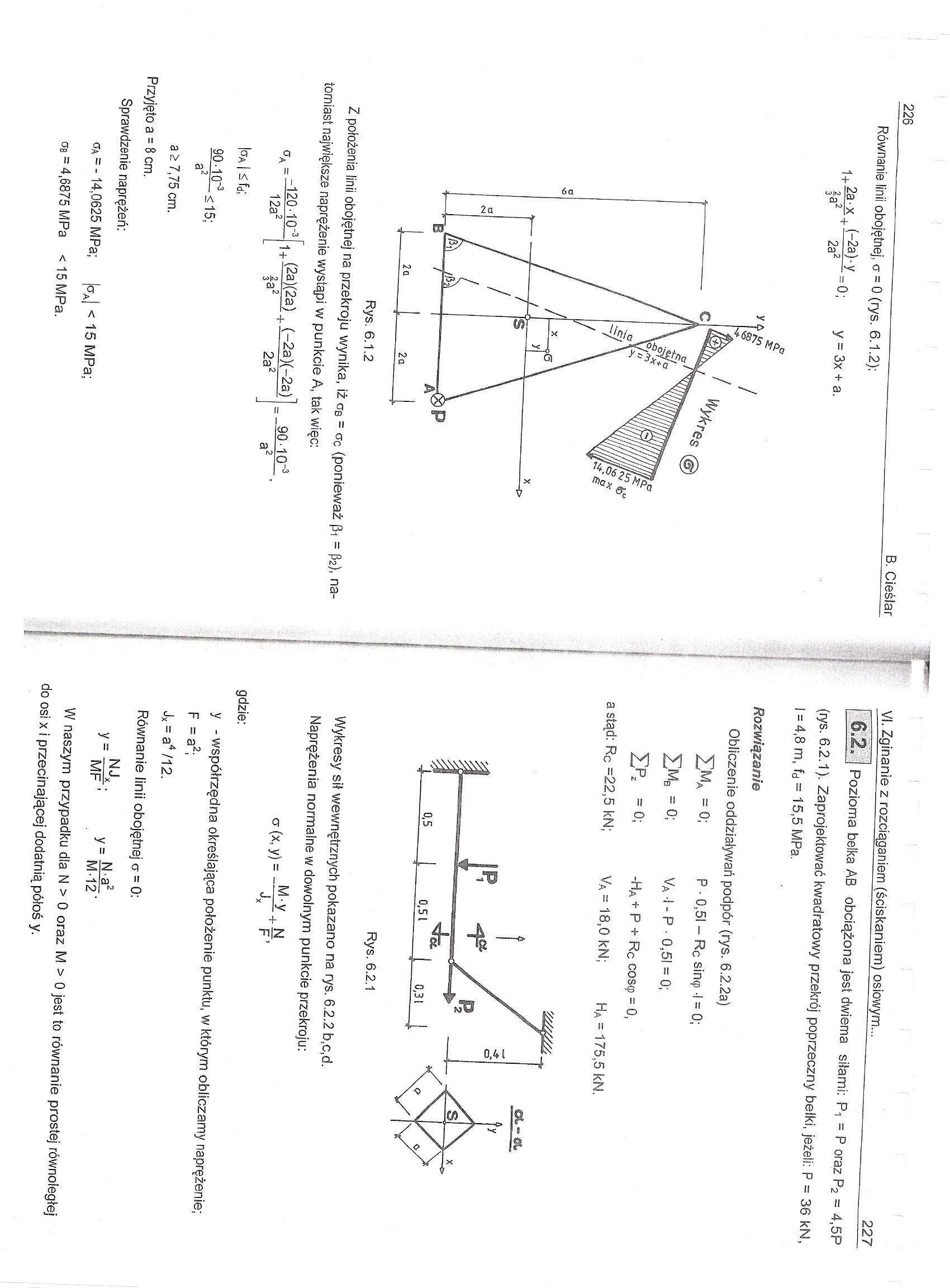
Równanie linii obojętnej, o m 0 (rys. 6.1.2):

1+^J<+l^hy₌o; y = 3x + a. fa 2a

Rys. 6.1.2

Z położenia linii obojętnej na przekroju wynika, iż ob = oc (ponieważ Pi = fc), natomiast największe naprężenie wystąpi w punkcie A, tak więc:

₁ (2a)(2a) (-2a)(-2a) la²    2a²

90 10~ a²

_ -120 -10~³ A 12a²

|ct_a | ^ fdl

90JOl_<1r. a²

a > 7,75 cm.

Przyjęto a = 8 cm.

Sprawdzenie naprężeń:

ga = -14,0625 MPa; |a_A] < 15 MPa;

a_B = 4,6875 MPa <15 MPa.

Pozioma belka ĄB obciążona jest dwiema siłami: Pi = P oraz P2 = 4,5P (rys. 6.2.1), Zaprojektować kwadratowy przekrój poprzeczny belki, jeżeli: P = 36 kN, I = 4,8 m, f_d= 15,5 MPa.

Rozwiązanie

Obliczenie oddziaływań podpór (rys. 6.2.2a) ]TM_a =0;    P • 0,5I -R_c sintp-I =    0;

£M_b =0;    V_A I-P- 0,51 = 0;

y.P_r — 0;    -H_a + P + Rc cos<p =    0,

a stąd: R_c =22,5 kN; V_A = 18,0 kN; H_A = 175,5 kN.

Rys. 6.2.1

Wykresy sił wewnętrznych pokazano na rys. 6.2.2 b,c,d. Naprężenia normalne w dowolnym punkcie przekroju:

<r(x.y) =

My

1

N

F’

gdzie:

y - współrzędna określająca położenie punktu, w którym obliczamy naprężenie; F = a²;

J_x = a⁴/12.

Równanie linii obojętnej <r = 0:

NJ_X MF ’

_ N a² M-12

W naszym przypadku dla N > 0 oraz M > 0 jest to równanie prostej równoległej do osi x i przecinającej dodatnią półoś y.