42364 skanuj0127 (12)

234 B. Cieślar

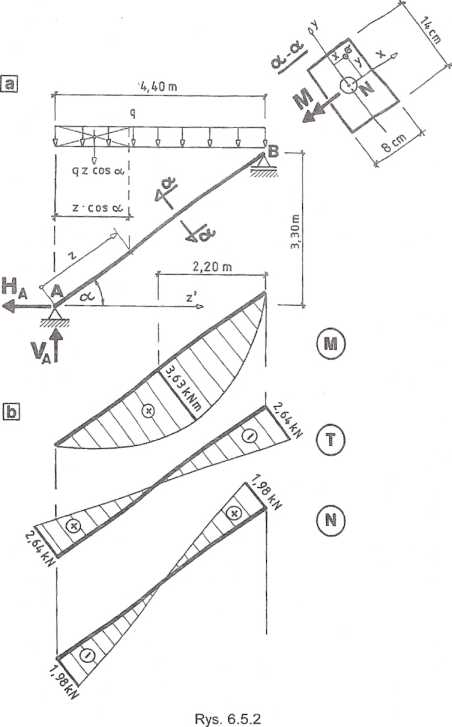
Tym samym największe naprężenia normalne otrzymamy dla y = 7 cm, będą to naprężenia ściskające. Na odcinku od połowy rozpiętości pręta do punktu B linia obojętna będzie również równoległa do osi „x”, lecz znajdować się będzie powyżej niej. Największe naprężenia otrzymamy dla y = - 7 cm, będą to naprężenia rozciągające. W każdym z powyższych przypadków naprężenia będą sumą składników o tych samych znakach. Gdyby na długości belki znajdował się przekrój, w którym równocześnie moment zginający i siła osiowa są największe, to w tym przekroju wystąpiłyby największe naprężenia normalne. Ponieważ ten przypadek nie zachodzi, to musimy zbadać, dla jakiej wartości "z" otrzymamy największą wartość naprężenia.

Odcinek I, ze (0; 2,75), y = 0,07 m.

^c(z>⁼ J2wśłmi¹    -10Q37,76z -176,786.

Szukamy ekstremum funkcji. o'= 3673,4z -10037,76;

c'(Zo) = 0;

Zo = 2,7325 m.

o(2,7325) =    -13,89087 MPa;

(o| = 13,89087 < f_d =15,5 MPa.

Odcinek II, z e (2,75;5,5), y = - 0,07 m.

, , _ (2.64Z - 0,48z² )(-0,07) (-1,98 + 0,72z) _ ^a{)~    0,0000182933    0,0112

= -1836,735z² + 10166,33z -176,786.

Ekstremum funkcji.

o'= - 3673,47z + 10166,33;

ff'(^zo) = 0;

Zo * 2,7675 m.

0(2,7675) =    = 13,89087 MPa < f_d = 15,5 MPa.

Sprawdzimy jeszcze wartości naprężeń na granicach obu przedziałów. o(0) = - 0,1768 MPa (w każdym punkcie przekroju);

0(2,75) * -13,89056 MPa (w punktach skrajnych); o(5,5) w 0,1768 MPa (w każdym punkcie przekroju).

VI. Zginanie z rozciąganiem (ściskaniem) osiowym...

235

6.6.

1

ściskające. Wyznaczyć rdzeń przekroju.