skanuj0124 (11)

228 B. Cieślar

Ac

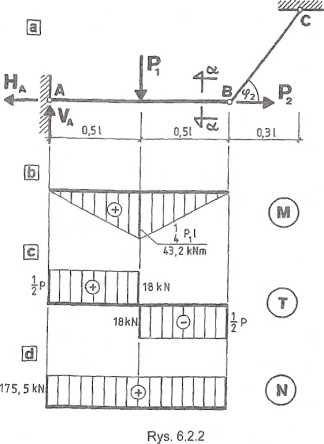
Największe naprężenie wystąpi zatem w punkcie I przekroju, w którym działają siły wewnętrzne M = 43,2 kNm i N = 175,5 kN.

43,2-10"³

Z

12

'•jam

2 ) , 175,5-10"

43,2-10~³ -6>/2 _| 175,5-10^-3 ^₁₅₅. a³    a²

15,5a³ 4175,5 ■ 10^-3 a - 43,2 • 10~³ • 6>/2 £ 0.

Powyższą, nierówność można rozwiązać w sposób ścisły lub metodą prób, tzn. podstawiać kolejne wartości „a” wiedząc, iż interesuje nas rozwiązanie dla a > 0. Dla kolejnych wartości „a” otrzymujemy następujące wartości lewej strony [L(a)] powyższej nierówności:

L(0,5)= 1,483;    L(0,4) = 0,555; L(0,3) = -0,000714;    L(0,31) = 0,041.

VI. Zginanie2 rozciąganiem (ściskaniem) osiowym...

229

Zakładając, iż wymiar „a” należało określić z dokładnością do 2 cm, jako rozwiązanie powyższej nierówności podajemy: a > 31 cm.

Zgodnie z narzuconą dokładnością przyjmujemy a = 32 cm otrzymując:

Cmax = <11 = 12,90 MPa < fd = 15,5 MPa.

Rozkład naprężeń normalnych pokazano na rys. 6.2.3.

6.3.

Słup jest obciążony mimośrodowo ściskającą siłą P (rys. 6.3.1). Sprawdzić,

czy naprężenia normalne nie przekraczają wytrzymałości obliczeniowej. Dane: b = 22 cm, h = 30 cm, P = 150 kN, fd = 15 MPa.

*4-~ i -4*

Rys. 6.3.1