skanuj0155 (11)

290 B. Cieślar

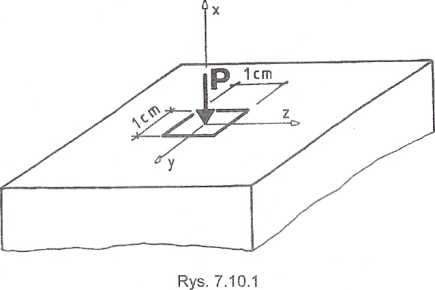
Rozwiązanie

Obliczamy naprężenie:

^0X= 0,01 0.01 ⁼ 0,0001 ^=_70MPa

Odkształcenia liniowe są równe:

Sy ⁼ £_Z ⁼ 0.

Równania fizyczne:

⁸y =jH^ay~<^CTx+«**];

⁸z =^Fz-(°x+^_y

a stąd

_v^ _ 0,3• (-70)

= -30 MPa.

y ^z 1—v 1-0,3

Wartości naprężeń głównych wynoszą: ai = - 30 MPa; a₂ = - 30 MPa; a₃ = - 70 MPa.

7 11. | Określić rodzaj stanu naprężenia, jeżeli jego składowe są równe:

c_x = 40 MPa;    <r_y = -100 MPa;    o₂ = 60 MPa;

ixy = - 50 MPa; x_xz = 80 MPa; x_yz = 20 MPa.

Rozwiązanie

Obliczamy wartości naprężeń głównych z równania: a³ — Si a² + S₂ a - S₃ = 0,

gdzie, na podstawie wzorów (1-2,1-3 i 1-4 - rozdz.l) mamy: Si = 40 + (-100) + 60 = 0;

S₂ =

s₃ =

40

-50

80

40    -50

-50 -100

	-100	20		40	80
+	20	60	+	80	60

-16900;

-50 80 -100 20 20 60

= 74000.

Po podstawieniu do równania wiekowego o³ - 16900 o - 74000 = 0

wyznaczymy wartości naprężeń głównych, będące pierwiastkami tego równania, metodą przedstawioną we wstępie do niniejszego rozdziału.

= 225,1666;

<j_h = fm )² - 3S₂]¹'² = [0 - 3(-16900)]^1/

cos 39 = ²⁷ •⁷⁴⁰⁰⁰ = 0,08751; ^v 2(225,1666)³

ę 5 0,4944.

Wartości naprężeń głównych: k = 1;

cti = | 225,1666 cos(- 0,4944) = 132,136 MPa;

k = 2;

a₂ = | 225,1666 cos(§ti - 0,4944) = - 4,383 MPa;

v    «J

k = 3;

a₃ = \ 225,1666 cos(f łt-2 - 0,4944) = - 127,753 MPa. O    o

Ponieważ wartości wszystkich naprężeń głównych są różne od zera, więc mamy w tym punkcie przestrzenny stan naprężenia.

7 12.

Określić rodzaj stanu naprężenia w punkcie A, jeżeli składowe są równe:

o_x = -100 MPa, o_y = 80 MPa, o_z = 50 MPa, Txy = 0, Txz = 0, Tyz = - 20 MPa. Powyższe składowe przedstawić na rysunku.