49558 skanuj0136 (11)

252 B. Cieślar

252 B. Cieślar

2. Obliczenie (Xo,y₀).

_x, _ 9a²(-a)+18a²(2a) ⁸    27a²

, _ 9a²(2a)+18a²(2a) ₂ 27a²

momentów bezwładności i momentu dewiacji względem osi centralnych

pkt.	Xo	yo	X	y	X	y
A	-a	4a	-3,349	2,406	1,090	-0,768
B	5a	-2a	5,108	1,706	-0,715	-1,084
C	-4a	-2a	-1,759	-4,112	2,075	0,450

Rys. 6.13.2

j,₌ą^₊M*£_=12t5a«_;

J_w=J35gąŁ₊(6ąM _{= 405a4;}

43*;

J_y< = J_y. - 27a²(a)² = 94,5a⁴;

= ^J»y ~ ²⁷a²(a)(2a)=-13,5a\

3. Określenie położenia osi głównych, centralnych.

tg2q>₀ =

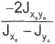
A-13,5a⁴) _ _e. 54a⁴ -94,5a⁴

<p₀=-40,27°+n-90°.

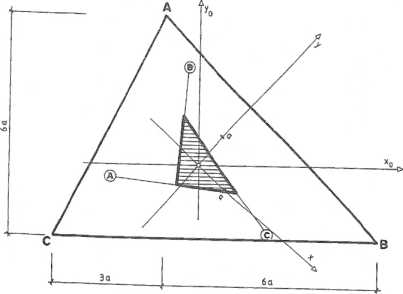
Rys. 6.13.3

VI. Zginanie z rozciąganiem (ściskaniem) osiowym...__253

4. Wartości głównych, centralnych momentów bezwładności.

J_ma> = J_y = 98,5875a⁴; i_y² = 3,6514a²; j_mh = j_x = 49,9125a⁴; i² = 1,8486a².

Obliczone, w układzie osi głównych, centralnych, współrzędne wierzchołków konturu przekroju (x, y) oraz współrzędne (x, y) punktów przecięcia się prostych ograniczających rdzeń z osiami głównymi, centralnymi (x, y) zamieszczono w tabeli na rys. 6.13.2, a kształt rdzenia pokazano na rys. 6.13.3.

Dane: rys. 6.14.1.

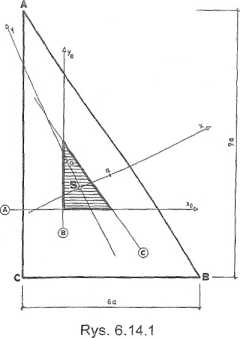
6.14.

Rozwiązanie

J_x> =121,5a⁴;

J_y-=54a⁴;

^Jx,y. = -40,5a⁴;

<P₀ = 25,10°; J_x=140,47a⁴;

J_y = 35,03a⁴;

F = 27a²; i_x² = 5,20a²; i² =1,30a².

Obliczone współrzędne (x,y) podano w tabeli, na rys. 6.14.2.

piet.	Xo	yo	X	y	X	y
A	-2a	6a	-0,734a	6,282a	-1,770a	-0,828a
B	4a	-3a	2,350a	-4,413a	-0,553a	1,178a
C	-2a	-3a	-3,083a	-1,868a	-0,422a	2,784a