skanuj0082 (29)

144 6. Cieślar

BO cm

Rys. 4.6.2

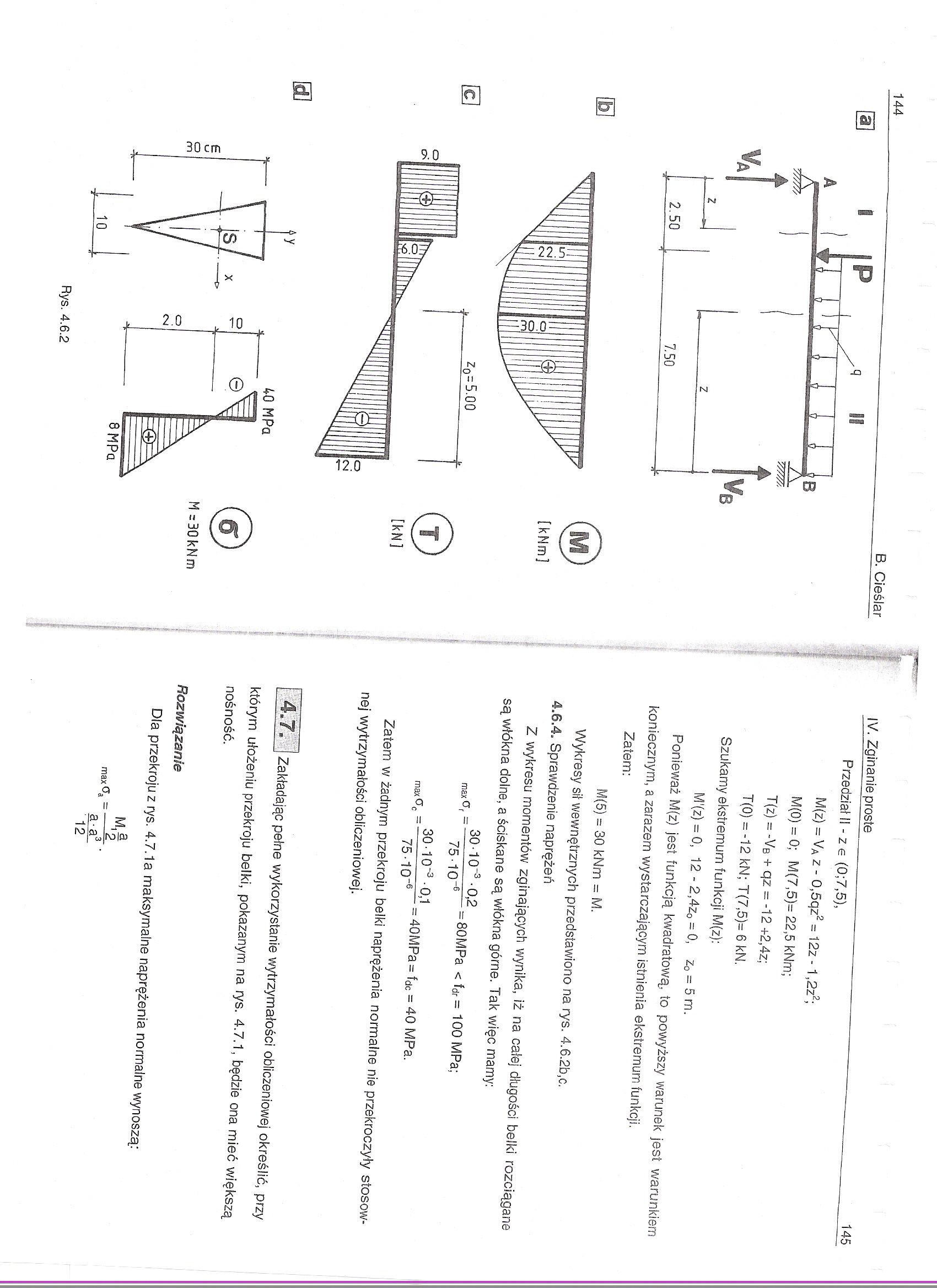
Przedział Ił - z e (0;7,5),

M(z) = V_A z - 0,5qz² = 12z -1.2Z²;

M(0) = 0; M(7,5)= 22,5 kNm;

T(z) = -V_B + qz = -12 +2,4z;

T(0) = -12 kN; T(7,5)= 6 kN.

Szukamy ekstremum funkcji M(z):

M'(z) = 0, 12 - 2,4Zo = 0, z₀ = 5 m.

Ponieważ M(z) jest funkcją kwadratową, to powyższy warunek jest warunkiem koniecznym, a zarazem wystarczającym istnienia ekstremum funkcji.

Zatem:

M(5) = 30 kNm = M.

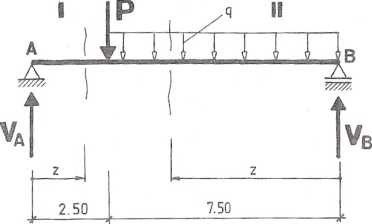
Wykresy sił wewnętrznych przedstawiono na rys. 4.6.2b,c.

4.6.4. Sprawdzenie naprężeń

Z wykresu momentów zginających wynika, iż na całej długości belki rozciągane są włókna dolne, a ściskane są włókna górne. Tak więc mamy:

30-10^-3 -0,2

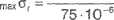
SO-10^0,1

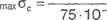
= 80MPa < fdr — 100 MPa;

= 40MPa=fdc = 40 MPa.

Zatem w żadnym przekroju belki naprężenia normalne nie przekroczyły stosownej wytrzymałości obliczeniowej.

| 4.7. Zakładając pełne wykorzystanie wytrzymałości obliczeniowej określić, przy którym ułożeniu przekroju belki, pokazanym na rys. 4.7.1, będzie ona mieć większą nośność.

Rozwiązanie

Dla przekroju z rys. 4.7.1 a maksymalne naprężenia normalne wynoszą:

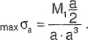
12