CCF20090522001

Punktowe grupy symetrii

Punktowa grupa symetrii - grupa, której elementami są operacje symetrii, a określonym działaniem ( 0) jest iloczyn tych operacji.

Grupa punktowa stanowi zbiór wszystkich punktowych operacji symetrii jakie można wykonać na danym przedmiocie.

Elementy symetrii odpowiadające tym operacjom symetrii przecinają się w jednym punkcie.

Grupy punktowe są grupami skończonego rzędu

7. A.Rybarczyk-Pirek

Symbol grupy punktowej (której elementami są operacje symetrii) powstaje przez podanie składających się na nią elementów symetrii

Przypomnienie:

Operacja symetrii (przekształcenie) jest jednostkowym działaniem (transformacją). Operacja symetrii: obrót, odbicie, inwersja

Element symetrii to obiekt geometryczny o specyficznych właściwościach - definiuje jakie operacje symetrii mają być wykonane. Element symetrii: oś czterokrotna, płaszczyzna zwierciadlana, środek symetrii

7. A.Rybarczyk-Pirek    8

Podstawowe elementy symetrii redukują się do następujących:

1, 2, 3, 4, 6, T, m(- 2), 3,4,6

Istnieją tylko 22 niezależne kombinacje elementów symetrii, co razem z 10 oryginalnymi elementami symetrii daje 32 możliwości

32 GRUPY PUNKTOWE

Elementami grup punktowych są operacje symetrii

Tożsamość pełni rolę elementu jednostkowego grupy punktowej

(dołączenie tożsamości do dowolnej operacji symetrii nie powoduje zmian)

7. A-Rybarczyk-Pirek    9

PODZIAŁ GRUP PUNKTOWYCH

1. Grupy punktowe z pojedynczym elementem symetrii X

Symbol grupy		elementy grupy (operacje symetrii)
1	=>	m
2	=>	{2; 2- = 1}
3	=>	{3;3^3; 3^3 = 1}
4	=>	{4; 4^2 = 2; 4^3;4^4=lj
6	=>	{6; 6^2= 3; 6^3= 2; 6^4= 3^2; 6^5; 6^6 = 1 }
i	=>	{i;i(= ni
m	=>	i^L^nP)} _
3	=>	{3 ;3 ;3 (= 1);3 ;3 ;3 (= 1
4	=>	{4 ;4^2( = 2);4^3;4^4( = 1)}
6		{6 ;6^2;6^3( = 3);6^4;6^S;6^6( =

Są to grupy cykliczne, wszystkie elementy każdej z nich można wyprowadzić z pierwszego elementu w zbiorze (zbiory tworzące)

7. ARybarczyk-Pirek    10

Grupa punktowa o symbolu: 6 {6; 6- = 3; 6³ = 2; 6⁴=3²;6⁵;6⁶ = 1 }

P₃

Jest to grupa:

>    6-cio elementowa (rząd grupy 6)

>    cykliczna (wszystkie elementy grupy p₄ można wyprowadzić z elementu 6¹, który stanowi zbiór tworzący {6}

r przemienna (kolejność działania nie ma tu znaczenia), bo: 6¹®6² = 6²®6^,= 6³ grupy punktowe cykliczne zawsze są grupami

Elementem jednostkowym jest tożsamość 1.

Dla każdego elementu grupy można znaleźć element odwrotny np. 6² i 6⁴ są dla siebie elementami odwrotnymi, ponieważ: 6² ® 6⁴ = 1

Rząd elementu:    6¹    wynosi    6    ponieważ (6¹ )⁶ = 1

6²    wynosi    3    ponieważ (6² )³ = 1

6³    wynosi    2    ponieważ (6³ )² = 1    ....

7. A.Rybarczyk-Pirek    11

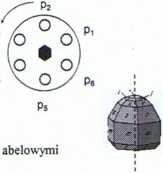
Grupa punktowa o symbolu: 3

{3 ;3^2;3^3( = i);3^4;3^5;3^6( =	i)i
Jest to grupa:
> 6-cio elementowa (rząd grupy 6)	^p'yx
> cykliczna (wszystkie elementy grupy
można wyprowadzić z elementu 3	lo
który stanowi zbiór tworzący {3}	^p5
> przemienna

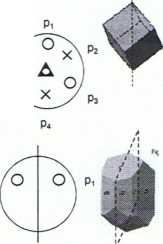
Grupa punktowa o symbolu: m {m; 1 (= m²)}

Jest to grupa:    p₂

>    2 elementowa (rząd grupy 2)

>    cykliczna (wszystkie elementy grupy można wyprowadzić z elementu m który stanowi zbiór tworzący {m}

>    przemienna

7. A Ryberczyk-Pirek