CCF2012121539

55

O

00000001010

11010100100011001100110010000000000000000000000

Rys. 2.10. Przykład zapis liczby rzeczywistej 425.1 w systemie cecha-mantysa

Liczbę rzeczywistą da się zapisać jedynie ze skończoną precyzją. W powyższym przykładzie nie udało się dokładnie zapisać liczby 0.1 ponieważ na 16-bitach udało się zapisać liczbę 0.0999908.

2.6. OPERACJE LOGICZNE

ALGEBRA BOOLE’A

Algebra Boole’a pozwala na operowanie na dwuelementowym zbiorze elementów {0,1}. Pozwala na budowanie wyrażeń logicznych, wykorzystujących dowolną liczbę zmiennych. Zasady algebry Boole’a stosowane są do wykonywania elementarnych operacji na bitach liczb binarnych.

Podstawowymi elementami algebry Boole’a są twierdzenia o sumie, iloczynie i prawa de Morgana. Ich składową są funktory.

PODSTAWOWE FUNKTORY LOGICZNE

Zarówno w informatyce, jak i ściśle z nią powiązanej elektronice (rys. 2.11), stosuje się następujące funktory logiczne (rys. 2.12):

•    NOT    - logiczne zaprzeczenie (x) np.:    dla    x    =    1,    x    =    0,    oraz

dlax = 0, x= 1,

•    AND    - iloczyn logiczny,

•    OR    -    suma logiczna,

•    XOR    - suma wyłączna (©),

oraz ich kombinacje np. NOR -> NOT OR, NAND -> NOT AND.

NOT    OR

-O— =E>

NOR

AND

O

NAND

XOR

O

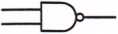
Rys. 2.11. Oznaczenia bramek wykonujących podstawowe operacje logiczne, stosowane na schematach układów cyfrowych