HPIM1054

m

W jakie) sksonomelrii rzutem sfery JcsŁ kote^-wojłhowrtj^^ kflwatcrsklcj. c) prostokątnej W których uksenomełnacH pewne płasxay2»^ ui^łndu są izomdrycine (odwaoggwąne -figury leży; na f|cl\ płaszczyznach lub równolegle do nich maj^ naturalny kształt): 3) pmwieprostokątnej^bwwjskow^ i kawalerskiej, d) izomefrii równokąłnej. d) prostokątnej

■

iwmnni rawncHcąrnej. aj prostokątnej.    -    x

^0M|p» Na jakiej płaszczyźnie układu dipnełrfi kawalerskiej należy przyjąć podstawę walca obrotowego, by jego konstrukcją była najprostsza o) yy. b) X2^>y2.

W ścianie pokoju znajdują się drzwi w kształcie prostokąta zakończonego półkolem. W przedpokoju świeci żarówka (punktowe źródło światła). Plama światła powstała na ścianie pokoju równoległej do ściany, w której znajdują s»e drzwi będzie^^/prosłokątem zakończonym półkolem, b) prostokątem zakończonym elipsą c) czworokątem o bokach nierówno ległych zakończonym parabolą.

\    y£fi/ii Ogniska elijpsy jeżą na: ą) na różnych osiadli na większy osi elipsy, c) na mniejszej osi elipsy.

_Jjb    WĘiM Elipsa ma'osie a ", b (a>6>ć). Oznaczmy odległość ognisk elipsy przez 2c (Ot>). Wówczas spełniony jest

urarunek: a) b+c.=<if}>lb * +c* ^o.* , c) b² +c³ =2a_

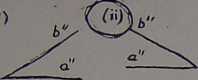
Na rysunku (fiys.1) mamy dwa rzuty kąta, który łworzą proste a, b, Rzeczywistą rozwartość kąta można bezpośrednio odczyta? z. rysunku^) (fi). t>) 0), C*»0_f c)

>q mm

^

Wom

m

Rys/J.

Rys.i

: !•-!
P> ' | .m __ jA	■ Nffi Ul	■ Ul H
3 X M -		( U| i

X W

Rys.^A

RysS

111

Wt

V

Uzupełnić konstrukcję rzutów punktów jednostkowych aksonometrii prostokątnej przy danym trójkącie śladów aksonotnelrycznych (K.ys.2)/

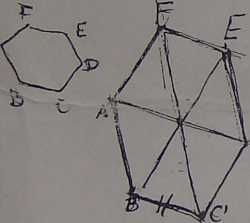
Uzupełnić rzut równoległy sześciokąla foremnego ASCDBF jeślf dane są rzuty A\ C* trzech kolejnych jego . wierzchołków/), 3, C (Rys.3). y^i5fv Rozwiązać fragment dachu z 'sąsiadem" (Rys*4).

Skonstruować obraz punktu wkołineaeji określonej przez tC.k.$ |§§ prosta graniczna) (Rys.S). di.O p rosłych. a( o.’, a." \ b (b‘, b^M) odwzorowanych w rzutach Monge'a wiadomo, że spełniają waruneka^oraz a?Ab\ Wtedy prostaa, b eta pewno są: a) równoległe/Cjtaiwnoległe lub skośne, c) identyczne (pokryutąją się).

43.f//" powierzchnia obrotowa powstaje przez obró* c^Ry 5, o której zakir»a:5iT.\', że jer. /.'CŻcna z toku okręgu i dwóch odcinków,dokoła prosty, która leży w płaszczyźnie obracanej krzywej,jest złożom z części powierzchni: ajtorusa lub sfery i dwóch stożków. b) totusa lub sfery < dwu hiperbolowl c)forusa lub sfery, Hipcrbołofdy i stożka.

\Ą '//•“' Dwie powierzchnie stopnia drugiego poznikają się w dwóch stożkowych (niez degenerowanych do pary prostych czy punktu). Aby Zawsae by+y fo elipsy (okręci) wystarczy założyć, że a) jedna z powieochni jed stoikiem, b) jedna a powierzchni jest walcem, c) obie powierzchnie są stoikami.

Mając kawałek sznurka, dwie szpilki i ołówek można rvarysow^ffi»el ipsę. b)olcpąę, cj hiperbolą.

Ą61Ii’¹ Rysując krzywą w zadaniu 15, szpilki wbijamy tv punkty, którcTftąją Się f^^^gniskami, b) wierzchołkami, c) Wieccchołkiem i ogniskiem otnry marnej stożkowej.

Ocena, sp£10~ nó<j. 10cif*.42~dsś. ^,lż<sp^ł4 -<lsH,tł<5|i^t6- db.łfics^fi *<tb+. W<spś^* bdh.