image20

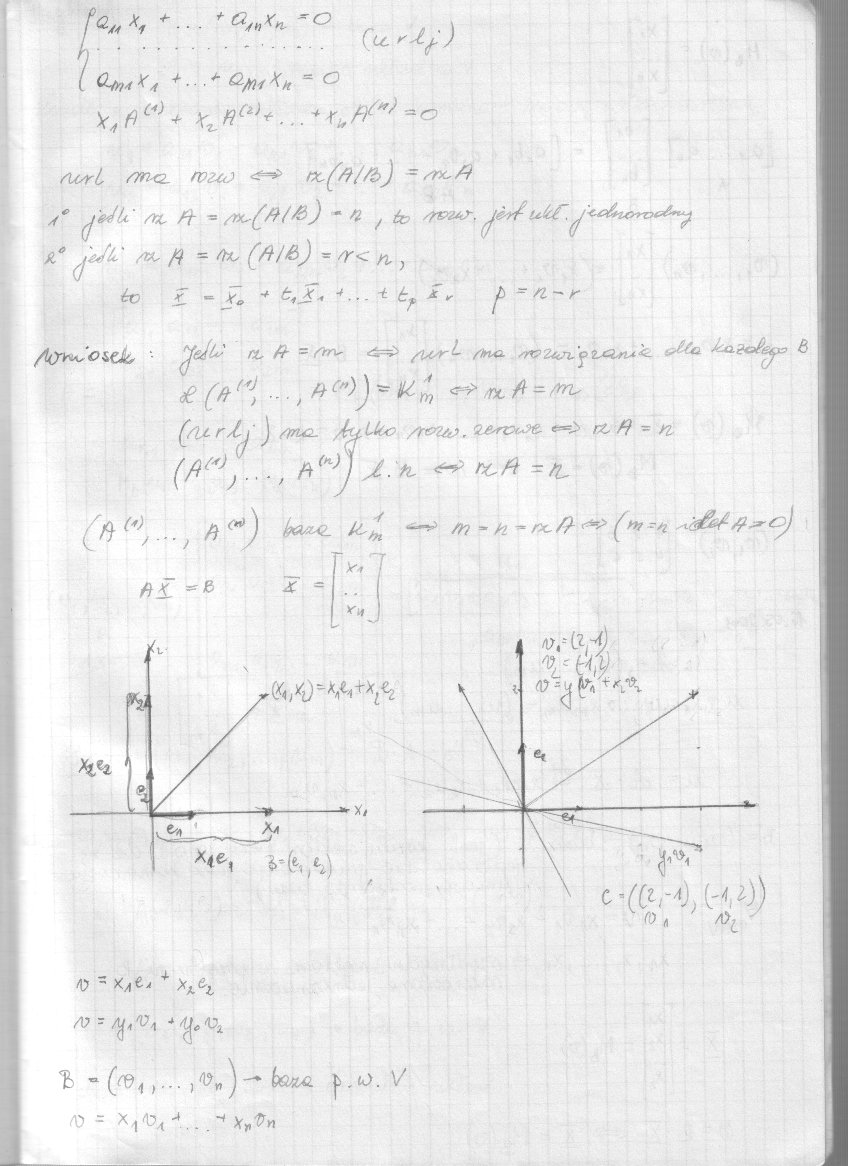
a„Xn-

d/y/4 %ą * • • • * Ą#/ %k ~ &

\. 0^C4) + ł; ^... ⁺ r. '/¥** -o

/z^r^ /Twe.    <^    Pc^/9//h) ” sno/j

4* ęj'&!L' rtL Ą -    ~ V , fo /T&Utr,    ^'<^ćnorc>eć~y

fi* ĄćJlc' /t^ /? = rtts (A/&) - /r< ^ _;

n.-r

jT - ^ + ć, j\, ⁴... ± bp * *    £

fi**))* Km *$_smLfi*mr

Strui. Uto /ir&?/t>' Z&r&cJe. e-0 rZ, - n

fl(y\r<*s O&Ck? '    ^ ^ ~    /U x~ ^ />K2. /t? 2^ć.t, 'Lsotru- <~ ‘?ćci ^Q.^c>be^ S

*(»">■

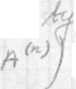
yi. fł, r^cft -Ą,

C^^rIj)

(**>-

,' f) ^j ... _t fi ^Ca>) k&uz. ii.^    /n *■ H ■*■ r*./?- <*& (»t ~*i

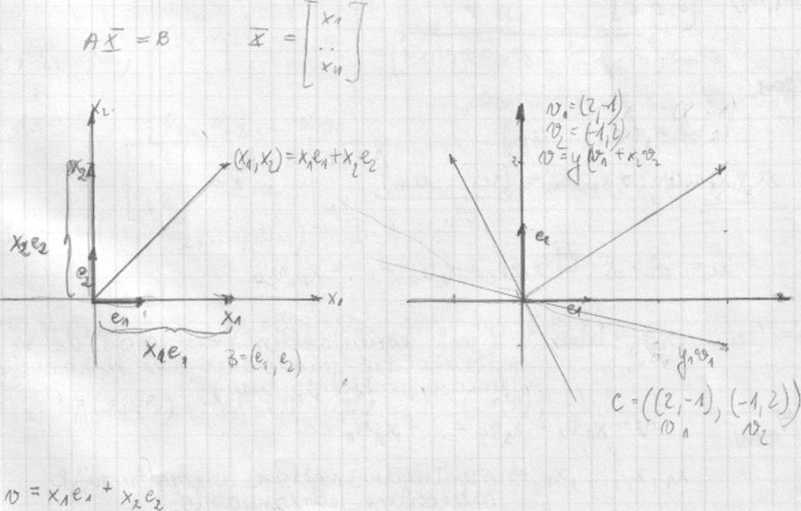
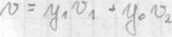
*& - (^rd_{Ą t}... ,^!^ ) -'* bztui j>. o. V

fO = ^X1^4 ^a..O x,Vn