Sieci CP str030

:jo

3.3. Uczenie pojedynczego neuronu

t^y*

,A.0) ...0)					. w w	(V
w, ws . .	Wn	wt Wg . .	■ Wn	. . .	w; Wg. .

T" T*

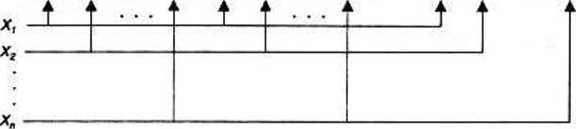
Wektor ten można wyznaczyć mnożąc wektor wejściowy X przez macierz W* o wymiarach [k x n], utworzoną w taki sposób, że jej kolejnymi wierszami są (transponowane) kolejne wektory    (dla m = 1,2.....k). Macierz W* ma więc następującą budowę;

k =

	„i" .
-!^!1		.. »?’
	-4*’ ■

W

Wykorzystując macierz W*, można zapisać funkcje realizowane przez całą sieć w formie jednego zwartego wzoru:

Y = W_k X

Wzór ten ujawnia jedną z podstawowych własności rozważanej tu sieci neuronowej: Otóż macierz W* zadaje określone odwzorowanie liniowe sygnału X 6 TZ'¹ w sygnał Y € 7?.*. Odwzorowanie to może być w zasadzie dowolne; jeśli przypomnimy sobie, że znaczna część używany cli w teorii przetwarzania sygnałów transformacji jest liniowa (na przykład transformacja Fouriera), wówczas łatwo zauważymy szeroką, praktyczną przydatność rozważanych tu sieci. Celowe jest tu także wprowadzenie jeszcze jednej interpretacji. Przekształcenie sygnału X w sygnał Y można traktować jako fili rację, w związku z czym o sieci neuronowej dokonującej takiego przekształcenia można mówić jako o filtrze. Taka interpretacja jest szczególnie wygodna przy omawianiu sieci MADALINE. o których będzie mowa dalej.

3.3 Uczenie pojedynczego neuronu

0 zachowaniu pojedynczego neuronu decydował wektor wag W, a o działaniu sieci macierz wag Wfc. Jak z tego widać wartości wag odgrywają w dziedzinie sieci neuronowych podobną rolę, jak programy w dziedzinie obliczeń numerycznych. Jak wiadomo programowanie systemów współbieżnych nastręcza wiele kłopotów, zatem zwykle bardzo trudne