Sieci CP str046

■i-10. Przyspieszanie procesu uczenia

momenł.nm):

.(rrOO + l)

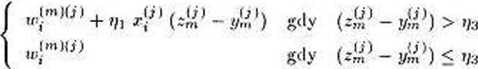
Z opisywanych w literaturze doświadczeń wynika, że parametr powinien na początku procesu uczenia przyjmować wartość 0,2, a następnie powinien być redukowany do zera [Klitna91].

Wybór współczynników ?/i, i r/_;i jest w chwili obecnej w większym stopniu sprawą sztuki (a więc na przykład intuicji eksperymentatora), niż sprawą ściślej wiedzy. Zwykle należy zaczynać od dużych wartości tych współczynników i potem stopniowo je redukować, czasami jednak proces uczenia lepiej przebiega, gdy w pierwszych krokach współczynniki te mają bardzo małe wartości, dopiero polem zwiększane są do typowego (wyżej podanego) poziomu. Jest to kwestia doświadczenia i wyczucia, gdyż trudno znaleźć teoretyczne uzasadnienie dla tego zjawiska. Podobnie powszechnie akceptowana empirycznie sprawdzona reguła, głosząca, że wymienione współczynniki powinny mieć mniejsze wartości dla dużych sieci (w sensie liczby neuronów), nie może być chwilowo przekonywująco wyjaśniona na podstawie czystej teorii, lima reguła, mająca duże znaczenie dla sieci złożonych z nieliniowych neuronów, głosi konieczność stosowania mniejszych wartości tych współczynników dla warstw sieci bliższych wejścia systemu i większych dla warstw dalszych — także nie całkiem wiadomo dlaczego, chociaż sam fakt nie podlega dyskusji.

Sejnowski i R.osneberg zaproponowali w 1987 roku jeszcze inną metodę przyspieszania procesu uczenia i polepszania jego zbieżności. Metoda ta, zwana czasem wygładzaniem wykładniczym, opiera się na wzorze podobnym w zasadzie do wzoru zawierającego mo-mentum, ale zakłada jącego nieco inne „ważenie" składników pochodzących od poprzedniej korekty wektora wagi i od określonego w kroku j błędu popełnianego przez sieć:

= Wl^j) + t_h [(i - ,,,) (Z^l» - YV>)[X⁽>>]^r+

Poważnym problemem przy uczeniu sieci neuronowych (nie tylko typu MADALINE) jest zapewnienie odpowiedniej randomizacji zbioru uczącego /•■'. Chodzi o to, że kolejne elementy < X#>, zw > powinny być losowo wybierane, a tymczasem z reguły ciąg uczący prezentowany jest cyklicznie, ponieważ liczba obiektów zarejestrowanych w tym ciągu (oznaczana A^r) jest zbyt mała w porównaniu z liczbą pokazów niezbędnych dla prawidłowego uczenia sieci. Można wprawdzie przed każdym cyklem mieszać starannie pokazy wchodzące w skład ciągu uczącego, ale nie zawsze daje to wystarczająco dobre rezultaty. W takim wypadku polepszenie efektów procesu uczenia można osiągnąć za pomocą kumulowania błędów. Technika ta polega na podzieleniu przedziału zmienności numerów obiektów ciągu uczącego j na odcinki o założonej długości ))ą (z praktyki wynika, że najlepsze wyniki daje 30 < i}^ < 50), ponumerowanie tych odcinków pomocniczymi indeksami j'[j* — 0. 1,2....) i obliczanie w każdym z tych odcinków pomocniczej wartości S^(; *

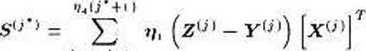
j=‘u ;’ + >