skanuj4

P = 20T = 20000kg

m

F = 20000kg -10 — - 200000N =&

parametrach: współczynnik rozszerzalności termicznej -

f^BC, moduł Younga

F - sili

A- przekrój pręrę

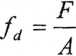
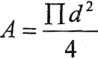
7. Podaj i objaśnij wzór na krzywiznę pręta zginanego

krzywizna pręta zginanego

210 MP a =

200kN

A =

A

200000N 210000000-Pa

(odwrotność promienia krzywizny) w zakresie sprężystym krzywizna ugiętej osi pręta jest

0,000952_OT² =9,52®E£Mffi-²J

^N M ^m    2

— = N--= m

Pa N

Ud²

4

= 9,52 -> d

9,52-4

n

proporcjonalna do sztywności zginania

moment zginający

3,48cm

ni którego

cm = cm

8.    Podaj i objaśnij wzór na odkształcenia przy czystym zginaniu.

_<T _ M

^    pr I    ^N'^e umiem zrobi

ĆT - odkształcenie E- moduł Younga M - moment gnący I - moment bezwładności

9.    Podaj i objaśnij wzór na naprężenia przy czystym zginaniu.

Czystym zginaniem nazywamy odkształcenie belki pomiędzy dwiema parami sił o równych momentach.

Przy czystym zginaniu w przekrojach poprzecznych belki nie ma naprężeń stycznych.

Obraz naprężeń normalnych przy czystym zginaniu

średnica = 2 • d =

6,9 6cm

płaszczyźnie przekroju poprzecznego

*przyjąłem przyciąganie ziemskie jako 10m/s^A2, możliwe że trzeba dać dokładniej 9,81m/s^A2

4. jaka siłą (wyrażoną w kNj można obciążyć pręt o przekrój u kwadratowym (długość boku 1 cal=25.4mm) fd=300MPa.

(gnący), moment, którego wektor działa w płaszczyźnie przekroju poprzecznego

sztywność zginania

iloczyn modułu Younga i głównego centralnego momentu bezwładności przekroju

Największe naprężenie normalne występuje we włóknach najdalej położonych od osi obojętnej przekroju poprzecznego:

M

a = —

/

Gdzie:

M - moment gnący,

I - moment bezwładności

10. Dobrać szerokość belki drewnianej o przekroju prostokątnym wysokość b-16 cm, przy zginaniu momentem M=12kNm. Wytrzymałość drewna przyjąć równą fd=11.0MPa

f =-

moduł sprężystości podłużnej

(Younga), stała materiałowa; tangens kąta nachylenia wykresu odkształcenia w funkcji naprężenia na

A = l² l = 25,4 mm = 2,54 cm = 0,0t^f>^iowej ^cz?^ści

wykresu rozciągania,

A— 0,0254² = 0,00064516/M ²    oznaczenie: E\ wymiar [Pa];

dla stali ok. 210 GPa

F = fi-■^A

F =300000000 • 0,00064516    = 193

N

F - sili której szukamy A - przekrój pręrę

Dane:

h = 16 cm (wysokość przyjmuję inna sygnaturę niż w treści zad aby było jasne o co chodzi)

M = 12 kNm fd = 1 IMPa

fd 1 f)M

bf

1Ó kN

6W„

=109,(MO⁶?.

^    ^u ''mm™ j2

_b=6fmęA₌6546^_5mj

Pa-m =

m

m

5. Pręt o powierzchni przekroju A=4cm2 i długości L=l,20m został włożony pomiędzy dwie podpory nieprzesuwne a następnie równomiernie ogrzany o AT=40⁹C. Wyznacz stan naprężenia w tym pręcie. Pręt został wykonany z materiału o następujących

6. Wyjaśnić jak przyjąć układ współrzędnych by rozwiązanie zagadnienie zginania przybierało prostą postać (jak wzory podane na wykładzie)

Według mnie trzeba przyjąć taki układ współrzędnych jaki był na wykładzie czyli:

ló    (cĄ²256

13. Od jakich wielkośći zależy położenie osi obojętnej przekroju mimośrodowego ściskanego lub rozciąganego?

Położenie osi obojętnej przekroju mimośrodowego zależy od wymiarów przekroju bryły (np. słupa) podanych w

#'    5    %