str055

,..|iuivymi.' spotur/iwniii un»o/liwiuJi|ł i •liikimiitm' takich prze kształceń, które prowadzą tlo wyrównania obserwacji synchtoitli/nycli i dwustron nycli metodą pośredniczącą. Oto tok wywodu.

Załóżmy, że kipy pionowe sieci pomierzono z jednakowi! dokładności.!, a zaobsei wowane odległości skośne S s;( traktowane jako wielkości stałe. Korzystając ze związku (3.21) można zestawić równania złożone dla każdej pary zaobserwowanch dwustronnie kątów. Ponieważ, współczynniki i wyrazy wolne równań złożonych obliczamy z dokładnością 3 do 4 cyfr znaczących, a kąty a"¹’ przyjmują niewielkie wartości, zachodzi przybliżony związek

^Sp '^c°s<« S_K • cosa°p ss Dr    (3.24)

który pozwala zapisać równania złożone w postaci

- ^KP + 57' ^VKP - ^dH, + ^dHK + AH- — AH_pK = O (3.25)

Zauważmy teraz (korzystając choćby z tablicy 3.24), że układ równań złożonych charakteryzują następujące właściwości, z których druga jest słuszna w tym przypadku, gdy spełnia się założenie jednakowej dokładności kątów sieci:

1)    poprawki v'_pKoraz v^_p kątów 1 -tego przęsła występują tylko w jednym, 1 -tym równaniu złożonym i w żadnym innym;

2)    współczynniki przy tych poprawkach są co do bezwzględnej wartości równe, lecz mają znaki przeciwne.

Z powyższych sformułowań wynika zaraz, że poprawki obu kątów przęsła są co do wartości bezwzglądnych równe, lecz mają znaki przeciwne, czyli

V¹ = — v'

KP    PK

Dla 1-tego przęsła zachodzą bowiem związki

(3.26)

^VPK = ^k*

(3.27)

KP

które świadczą o słuszności wypowiedzianego stwierdzenia.

Jeżeli z równań (3.25) wyłączymy wszystkie kolumny zawierające współczynniki przy poprawkach v_Kp, a każdy współczynnik przy poprawce v_pK pomnożymy przez sjl, otrzymamy układ równań złożonych postaci

-77^ł'^V|.K-<^IHr + ^dHK + AC-AH_pl<-0    (3.28)

w których nie występują już poprawki v_Rp. Jest przy tym oczywiste, że równania normalne zestawione na podstawie przekształconych równań złożonych typu (3.28) będą miały identyczną tabelę z tymi, które zestawilibyśmy z równań złożonych nie przekształconych (3.25). 1-ty element przekątny, przekątnego bloku (ta )², obliczony / rów nu ń nic przekształconych, hęd/ii hms u m .mmi kwmlnilów obu współczynników pr/y poprawkach I-tego równaniu /lo/onego. czyli

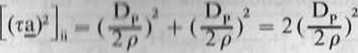
(.1.29

natomiast odnośny element bloku (rą')², obliczony z równań przekształconych, będ/ń kwadratem jedynego współczynnika przy poprawce V , a więc

(\ )0

Ponieważ omówione przekształcenie nie zmienia bloków d oraz m (kolumn, wyrazów wolnych), wynika stąd, że równania normalne

rk    rdH    1

(rą)²    d    co    (3.11

rd    0    0

otrzymane z wyjściowych i przekształconych równań złożonych będą miały idcnlyezn tabele układu. W konsekwencji rozwiązanie tych równań da takie same warlośi korelat k oraz niewiadomych dH.

Jeśli jednak zechcemy obliczyć poprawki V_|>K z przekształconych równań zlo/_t nych na podstawie związku V = k-a', to otrzymamy

=    w:

podczas gdy z równań wyjściowych mielibyśmy

vL = k

<-f>

2 p

(3.3

Zachodzi więc relacja

v

albo

PK -jT

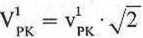
(3.3*

(3.3:

pozwalająca obliczyć poprawki obserwacyjne v_pK na podstawie poprawek V₍ obliczonych z równań przekształconych. Poprawkę obserwacyjną v‘_pK drugiego kip 1-tego przęsła obliczmy, oczywiście, korzystając ze związku (3.26).

Całe dotychczasowe rozumowanie mające na celu ustalenie związków międ< poprawkami obserwacyjnymi v_pK, v_Rporaz poprawkami V_pK występującymi w ró\ naniach złożonych przekształconych, przeprowadziliśmy przy założeniu, że sit podlega wyrównaniu metodą zawarunkowaną z niewiadomymi. Zauważmy jednak, w każdym przekształconym równaniu złożonym występuje tylko jedna poprawka V_p W takim przypadku w elementarny sposób można przejść od równań złożonyi