Zdjęcie 0088

> local x,y,j:
> x[0]:=x0: y[0]:=y0:
> for j from 1 to N do
> x[j] :=evalf (rho*y[j-l]) :
> y[j] :=evalf (r*x[j-l]*(l-x[j-l]/a)) :
> end do:
> plots[pointplot](seq([y[k],x[k]],k=i..N),symbol=point);
> end proc:
> salmon(.7,5.7,l,.7,.9,100000);
24. Niech populacja X rozwija się zgodnie z modelem Verhulsta, przy czym w każdym pokoleniu dokonujemy pewnego odłowu Hn :
Xn+\ ^
rXn Xn + A
Hn.
Przeanalizować, jaki maksymalnie może być odiów, aby populacja nie wymarła.
25. Rozważmy model rozwoju epidemii Kermacka-McKendricka. Niech Sn oznacza liczebność grupy podatnych na chorobę, /„ 1 zarażonych, a Rn - tych, którzy nabyli odporność. Zakładamy, że r- choroba nie jest śmiertelna tzn. Sn + In + Rh = N - stała wielkość całej populacji,
%1 = (1 ~P)U,
Un
gdzie p oznacza prawdopodobieństwo kontaktu chorego z podatnym,
= 1 - (1 -P)1"-
Oznaczmy przez e~° liczbę 1 — p. Zapisać wzór na układ dynamiczny w M3 opisujący te zależności. Pokazać dodatnią niezmienniczość zbioru [0, oo)3, a także zbioru
K := {(S,/)€ R2: 5 > 0, / > 0, S + I<N)
względem układu zredukowanego do pierwszych dwóch współrzędnych. Zbadać ten układ. W szczególności poszukać warunków, przy których następuje wygaśnięcie epidemii.
26. Zbadać układ zadany w R2 przez odwzorowanie
r m
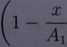
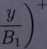
ML
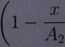
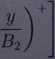
5
Wyszukiwarka
Podobne podstrony:
Zdjęcia 0088 i ‘H t p dH*. ł T , g&C t: ;
Zdj?cia 0088 (2) Nazwa ogólna: azwa powdyi co najmniej (hu dc$>giuiy
Zdjęcia 0088 (5) wapń***»>»&, *•*’"” * * «** 4** i.uI * • ( a w organizmie pełni role:-
19986 Zdjęcia 0088 (5) wapń***»>»&, *•*’"” * * «** 4** i.uI * • ( a w organizmie pełni r
Zdj?cia 0088 Nazwa ostra1 To nazua. która ma ostry zakres, un jednoznacznie można rozstrzygnąć, e/ d
Zdjęcia 0088 s,nU00r) ,K 811.1 11 R 4 /reali ».l clek«njniwn; tt ---■ .... 1=1 5.0
Zdjęcia 0088 (4) Definicja przeciw utleniacz , Przeciwutieniaczcm jest każda substancja. ktńrjj V v
skanuj0021 (15) dwuocznego widzenia przestrzennego, wyk. 2 zdjęcia z 2 różnych stanowisk między nimi
eventviewer E Event Viewer File Action View HelpO ^ UD £0 Hf [?) B3> $ jTjjJ Event Viewer (Local)
więcej podobnych podstron